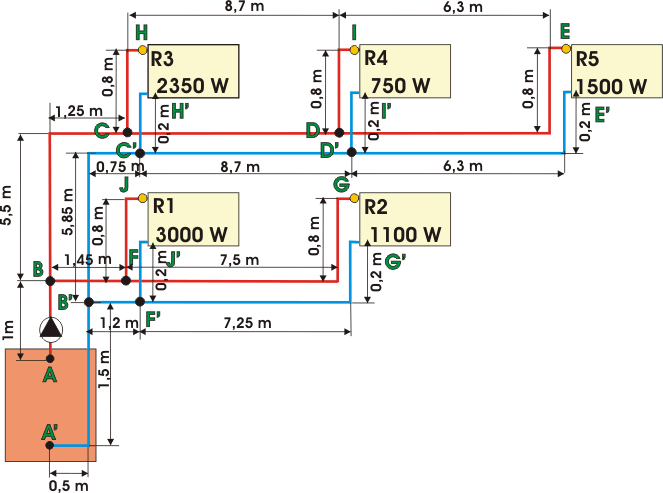
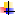>>

LES RADIATEURS

 

 

Perte de charge et diamètres

Connaître diverses valeurs d'un radiateur

 

puce Dimensionnement des radiateurs.
Pour le dimensionnement d'un radiateur, les déperditions thermiques (voir les pages qui traitent du calcul des déperditions) de la pièce dans laquelle il va se trouver doivent avoir été calculées. Une fois ces déperditions obtenues, vient le choix du radiateur. Ce choix va être fait dans le catalogue d'un fabricant. Il faut savoir que les puissances annoncées sur les catalogues sont des puissances "normalisées" c'est à dire qu'elles ont été mesurées suivant une méthode bien précise (méthode décrite dans la norme européenne EN 442). En gros, les émissions thermiques d'un radiateur sont mesurées dans une cellule de 4m x 4m x 3m maintenue à une température ambiante (Ti) de 20°C par refroidissement de ses parois et ceci par circulation d'eau. La température d'entrée d'eau du radiateur (Te) est portée à 75°C puis le débit est réglé de façon à obtenir une chute de température dans le radiateur de 10°C donc 65°C en sortie de radiateur (Tr) et ceci afin d'obtenir un DeltaT de 50 °C : (75 + 65) / 2 - 20 = 50 , une fois les températures stables, on mesure à l'aide de différents capteurs la puissance thermique totale (radiative et convective) du radiateur. Avec le même débit la puissance est mesurée à différents DeltaT. Plusieurs radiateurs sont mesurés dans une même gamme et pour connaître la puissance émise par tous les radiateurs de la gamme on procède par méthode d'interpolation. Avant le 28 septembre 1997 la norme Française (NF P 52011) était appliquée. La différence entre les 2 normes est principalement le DeltaT utilisé : NF P 52011 DeltaT = 60 °C (90 + 70) / 2 - 20 = 60, EN 442 DeltaT = 50 °C (75 + 65) / 2 - 20 = 50. Cette baisse de température pour le calcul des puissances des radiateurs est principalement due aux températures de fonctionnement des chaudières actuelles, généralement limitées à 75°C, qui fonctionnent en basse et très basse température car les logements sont maintenant très bien isolés et ne demande donc plus des températures élevées.
Le choix du radiateur dans un catalogue se fait généralement par valeur égale ou supérieure à la valeur des déperditions. Comme les déperditions ont été calculées dans les conditions de base (températures extérieures constatées au moins 5 fois dans l'année et ceci sur plusieurs années), si on prend un radiateur qui correspond de très près à la puissance nécessaire et que la température de base est dépassée durant quelques jours, les déperditions seront supérieures à celles calculées et comme la chaudière est déjà au maximum de ses possibilités avec les conditions de base (température de départ de 75 °C) les émissions seront inférieures aux déperditions et la température d'ambiance va descendre jusqu'à ce que les déperditions soient en équilibre avec les émissions thermiques du radiateur. Pour cette raison il est conseillé de rajouter une marge de puissance au radiateur de 15 à 20% si on n'utilise pas le radiateur en basse température (voir ci-dessous) : déperditions x 1,15 ou 1,20. Il faut aussi savoir que plus la température de départ chaudière devra être élevée moins bon sera le rendement de l'installation.
 
puce Précisions sur les radiateurs.
Un émetteur transmet sa chaleur par rayonnement et par convection dans une proportion qui dépend des températures de départ, de retour et d'ambiance, de la géométrie de cet émetteur, de l'état de sa surface (peinture, etc...), ainsi que de sa position dans le local où il se situe. Ce rapport est symbolisé par le coefficient n qui représente la loi d'émissions de l'émetteur. Plus la quantité de chaleur émise par rayonnement est importante, plus la valeur de n est faible. La valeur de n augmente avec la hauteur de l'émetteur. Cette valeur varie entre 1 et 1,5, 1 à 1,1 pour un émetteur transmettant principalement sa chaleur par rayonnement (cas des planchers et plafonds chauffants) et 1,4 à 1,5 pour un émetteur transmettant sa chaleur principalement par convection (cas des convecteurs) avec une valeur généralement situé entre 1,20 et 1,30. Ce coefficient est souvent indiqué dans le catalogue du fabricant mais dans le cas contraire, pour un radiateur, la valeur de 1,287 peut être utilisée avec suffisamment de précision.
Note : il faut savoir que le coefficient n varie d'un type de radiateur à un autre et même au sein d'une même gamme.
 
puce Transmission par rayonnement.
La transmission thermique par rayonnement s'effectue par rayonnement électromagnétique et n'a pas besoin de matière pour se propager (le rayonnement solaire).
La quantité de chaleur transmise par rayonnement est calculée avec la formule suivante :
Qr = S x hr x (Tm - Ti)
S est la surface d'échange thermique de l'émetteur, en m²
hr est le coefficient de transmission thermique par rayonnement, en W/(m².K) et s'obtient de la façon suivante :
hr = Ec x (T1 + T2) x (T12 + T22) x Co
Ec est l'émissivité de la surface qui vaut 1 pour un corps noir et qui est comprise entre 0 et 1 selon l'état de surface du matériau. Dans les locaux d'habitation les surfaces peuvent être considérées comme des corps noirs et la valeur de Ec est peu différente de l'unité mais la valeur moyenne pour Ec peut être prise égale à 0,9.
T1 et T2 sont les températures absolues, en K, des corps en présence, T1 pour la température moyenne de l'émetteur et T2 pour la température du local car on part de l'hypothèse que toutes les parois et objets sont à la même température que la température ambiante du local.
Co est la constante de Stefan-Boltzmann, et vaut 5,67051 x 10-8
Tm est la température moyenne de l'émetteur, en °C
Ti est la température ambiante de la pièce, en °C
 
puce Transmission par convection.
La transmission thermique par convection s'effectue par un mouvement des molécules d'air. Pour le cas des radiateurs, la convection est naturelle (libre) et l'échange de chaleur est responsable de ce mouvement. C'est le transfert de chaleur qui provoque le mouvement de ces molécules par la différence de densité qui est fonction de la température.
La quantité de chaleur transmise par convection peu être calculée avec la formule suivante :
Qc = S x hc x (Tm - Ti)
S a la même signification que précédemment
hc est le coefficient de transmission thermique par convection, en W/(m².K) et peut être obtenu, pour un radiateur classique, avec la formule suivante (cette formule est empirique car le phénomène est plus complexe qu'il y paraît) :
hc = 5,6 x ((T1 - T2) / (T2 x h))0,25
T1 et T2 ont la même signification que précédemment
h est la hauteur de la surface de chauffe, en m

Note : ces formules permettent de calculer la puissance approximative d'un radiateur mais ne permettent en aucun cas de les indiquer à des fins commerciales.

Prenons un exemple pour calculer les émissions thermiques totales d'un radiateur (Qt).
La surface d'échange thermique de ce radiateur est de 2,5 m², sa hauteur est de 0,85 m, la température moyenne du fluide caloporteur est de 70 °C et la température du local est de 20 °C :
hr = 0,9 x (343,15 + 293,15) x (343,152 + 293,152) x (5,67051 x 10-8) = 6,614 W/(m².K)
Qr = 2,5 x 6,614 x (70 - 20) = 826,75 W
hc = 5,6 x ((343,15 - 293,15) / (293,15 x 0,85))0,25 = 3,748 W/(m².K)
Qc =  2,5 x 3,748 x (60 - 20) = 468,50 W
Qt = 826,75 + 468,50 = 1295,25 W

Les émissions calorifiques sont caractérisées par un coefficient de transmissions thermiques (K) en W/(m².K). La valeur de ce coefficient est fonction de l'écart moyen des températures (température moyenne de l'émetteur moins la température ambiante du local à proximité de cet émetteur), de ce fait, cette valeur est variable mis à part pour les planchers et plafonds chauffants où elle est supposée constante donc indépendante de cet écart moyen des températures, ce qui est très près de la réalité.

Ci-dessous deux graphiques montrant les valeurs de hc et hr.
Le graphique 1 indique les valeurs des coefficients hr et hc pour une hauteur de radiateur de 1 m
Le graphique 2 indique les valeurs du coefficient hc en fonction de la hauteur du radiateur pour un DeltaT de 50 °C. hc diminue avec la hauteur.



L'équilibre thermique de l'ensemble local-émetteur, en régime permanant, est donné par la relation suivante :
Q = K x S x (Tm - Ti) = H x (Ti - Te) = D x 1,1628 x (Td - Tr), en W
où :
S est la surface d'échange thermique de l'émetteur, en m². Cette surface est difficile à définir, pour la connaître, il est possible de l'obtenir auprès du fabricant.
H est le coefficient de déperditions thermiques par transmission et par ventilation, en W/K (voir la partie "Déperditions thermiques")
D est le débit de fluide caloporteur, en litres/h. (Pour plus de précision, utiliser le débit en kg/h)
Td est la température du fluide à l'entrée de l'émetteur
Tr est la température du fluide à la sortie de l'émetteur
Te est la température extérieure.
Le coefficient K, pour un DeltaT autre que le DeltaT nominal, est obtenu avec la formule suivante :
K = KN x (DeltaT / DeltaTN)(n - 1), en W/(m².K)
où KN est le coefficient K nominal obtenu lors des essais pour déterminer la puissance de l'émetteur. Si on connaît de façon précise la surface d'échange thermique de l'émetteur il est possible d'obtenir le coefficient K nominal de l'émetteur de la façon suivante :
KN = Q / DeltaTN / S
Q étant la puissance de l'émetteur, en W
DeltaTN est le DeltaT normalisé, actuellement 50 °C.
En prenant le résultat de l'exemple ci-dessus, le coefficient KN est égal à :
KN = 1295,25 / 50 / 2,5 = 10,362 W/(m².K)
 
puce La chaleur douce.
On appelle radiateur à chaleur douce ou radiateur basse température un radiateur qui fonctionne à un DeltaT inférieur à celui normalisé (50°C).
Les avantages sont :
- Les pertes thermiques réduites : déperditions des conduites, de la chaudière et des différents organes réduites car elles sont fonction de l'écart moyen des températures. Il en est de même pour les pertes thermiques au dos des émetteurs se trouvant sur les murs extérieurs.
- Homogénéité de l'ambiance (gradient de température plus faible).
- Moins de convection donc moins de poussière en mouvement.
- Réserve de puissance dans les cas de températures extérieures exceptionnelles, on augmente plus facilement la puissance d'un radiateur avec la température du fluide qu'avec le débit car la puissance chute dans les faibles débits mais augmente peu dans les forts débits.
- meilleur rendement de l'installation.
Les inconvénients sont :
- Radiateur plus grand donc coût plus élevé.
- Emprise sur les murs plus importante.
- Volume d'eau plus important, ce qui va influer sur le volume du vase d'expansion.
Le DeltaT que l'on peut utiliser se situe généralement entre 30 et 50°C. Il est bien évidemment possible de descendre en dessous 30°C mais dans ces conditions la taille du radiateur sera conséquente ou alors il faudra adopter une chute assez faible ce qui induira une perte de charge plus importante et donc, un circulateur plus puissant.
Le problème pour l'emploi d'un radiateur en chaleur douce est de connaître la puissance qu'il développe à un DeltaT différent de 50°C. Pour cela, il faut utiliser la formule suivante :
Q = Dep / (((Td - Tr) / ln((Td - Ti) / (Tr - Ti))) / DeltaTN)n
(La formule ci-dessous permet de savoir la puissance développée par le radiateur en fonction du DeltaT)
Q = Dep x (((Td - Tr) / ln((Td - Ti) / (Tr - Ti))) / DeltaTN)n
Q = puissance du radiateur qu'il faudra choisir dans le catalogue du fabricant par valeur égale ou supérieure.
Dep = déperditions thermiques de la pièce qui sont considérées comme correspondantes à la valeur normalisée d'un radiateur dans le catalogue.
La température du fluide à l'entrée du radiateur est générale à l'installation car donnée par la chaudière (Température de départ Td). Petite précision, un supplément de débit d'environ 20% devra être rajouté au débit du radiateur afin que la température d'entrée soit respectée et ceci pour prendre en compte les pertes en ligne (déperditions des conduites, etc...).
ln = logarithme népérien pour prendre en compte l'écart moyen des températures non pas arithmétique mais logarithmique et ce plus particulièrement lorsque les écarts de température sont assez importants, C < 0,7 :
C = (Tr - Ti) / (Td - Ti)
Exemple :
De = 1245 W
Td = 60°C
Tr = 50°C (chute de 10°C entre Td et Tr)
Ti = 20°C
DeltaTN = 50 °C
n= 1,287
Q = 1245 / (((60 - 50) / ln((60 - 20) / (50 - 20))) / 50)1,287 = 1988
Afin de développer la puissance de 1245 W, le radiateur à choisir dans le catalogue devra avoir une puissance égale ou supérieure non pas à 1245 W mais à 1988 W. Le DeltaT (écart moyen des températures logarithmique) est de 34,76°C au lieu de 50°C. Dans cet exemple la température de départ chaudière dans les conditions de base sera de 60°C au lieu de 75°C d'où une économie d'énergie.
Si le radiateur est conservé, sa puissance réelle sera non pas de 1245 W mais de :
Q = 1245 x (((60 - 50) / ln((60 - 20) / (50 - 20))) / 50)1,287 = 780 W

Il est aussi possible d'utiliser l'écart moyen arithmétique des températures pour simplifier les calculs mais ceci quand les écarts de températures Td-Tr sont faibles (chute < 20 °C), dans ce cas, la formule à utiliser est la suivante :
Q = Dep / ((((Td + Tr) / 2) - Ti) / DeltaTN)n
Avec les mêmes données de l'exemple ci-dessus :
Q = 1245 / ((((60 + 50) / 2) - 20) / 50)1,287 = 1970 W
En conservant le radiateur :
Q = 1245 x ((((60 + 50) / 2) - 20) / 50)1,287 = 787 W
Pour prendre en compte la variation du coefficient K, il est préférable d'utiliser l'écart moyen logarithmique des températures (plus près de la réalité) surtout si le débit est faible (chute importante), le graphique ci-dessous représente l'augmentation de puissance en fonction du débit avec :
- l'écart moyen logarithmique des températures (courbe bleu)
- l'écart moyen arithmétique des températures (courbe verte)
Ce graphique a été tracé avec une puissance de 1000 W et une température de départ de 75 °C.
On voit bien que dans les faibles débits l'écart de puissance est non négligeable entre les deux courbes et c'est seulement quand le débit approche 45 l/h (chute d'environ 20 °C) que les courbes commence à ce rejoindre. Conclusion, si on applique l'écart moyen arithmétique des températures à un radiateur ayant un débit plus faible que le débit normalisé la puissance indiquée sera surestimée par rapport à la réalité et cet écart se creusera avec l'augmentation de la chute (réduction du débit).



 
puce Chute de température dans le radiateur.
Les émissions thermiques d'un radiateur sont fonction de l'écart moyen (il est possible de prendre l'écart moyen arithmétique pour simplifier les calculs des températures (Td + Tr) / 2 - Ti ), plus il est important plus les émissions sont importantes. La température de départ est commune à tous les radiateurs car donnée par la chaudière (aquastat ou régulation).
La chute de température est la différence (DeltaT) entre la température à l'entrée du radiateur et celle à la sortie de celui-ci. La chute normalisée est maintenant de 10°C mais la profession utilise en règle général une chute de 15°C car de cette façon les débits sont plus faibles ce qui réduit les pertes de charge (voir plus bas), mais comme l'utilisation d'une chute plus grande va induire un écart de température plus faible Tm - Ti ( Tm étant la température moyenne du radiateur, Tm = (Td + Tr) / 2), la puissance du radiateur sera elle aussi plus faible, il faudra dans ce cas augmenter sa taille pour compenser cette perte. Exemple avec une chute de 15 °C :
Td = 75 °C donc valeur normalisée
Ti = 20 °C, idem
Tr = 75 - 15 = 60 °C et non 65 °C
Donc, la puissance du radiateur à prendre dans le catalogue du fabricant pour développer les 1245 W nécessaires sera de :
Q = 1245 / (((75 - 60) / ln((75 - 20) / (60 - 20))) / 50)1,287 = 1345 W, DeltaT = 47,10°C au lieu des 50 °C normalisés.
Là, on voit que la chute plus importante (5 °C)  induit une perte de puissance de 100 W.
Dans la même idée, avec une chute plus faible que celle normalisée on pourra réduire la puissance du radiateur, exemple avec une chute de 7°C :
Q = 1245 / (((75 - 68) / ln((75 - 20) / (68 - 20))) / 50)1,287 = 1201 W, DeltaT = 51,42°C au lieu de 50°C.
Là, le gain est de 44 W.

Par habitude, on utilise une chute identique pour tous les radiateurs (15°C) mais ceci n'est pas une obligation car elle peut être différente pour chaque radiateur et de cette façon on peut jouer sur les débits et sur les tailles des radiateurs afin de palier à certains petits problèmes comme par exemple un radiateur assez éloigné de la chaudière pour lequel il est difficile d'avoir un diamètre de conduite en rapport du débit donné avec une chute de 10°C en adoptant une chute plus importante on réduit le débit nécessaire et donc le diamètre et par la même, la perte de charge mais en contre partie il faudra augmenter sa taille.
Pour connaître le débit nécessaire en fonction de la puissance il faut utiliser la formule suivante :
Q / (DeltaT x c x p)
Q = puissance du radiateur
p = masse volumique de l'eau en kg/litre en fonction de sa température (voir le tableau à la page "Formules/Tableaux") p doit être pris à la T° moyenne du radiateur : (Td + Tr) / 2
c = coefficient de chaleur spécifique de l'eau c = 1,1627. (1 Wh = 3600 J, 1 Kcal = 4185,5 J, c = 4185,5 / 3600 = 1,162638889 W)
Pour simplifier les calculs il est possible de prendre un coefficient (dans le cas ou la chute est identique à tous les radiateurs) : Ce = 1 / (DeltaT x c x p) et ensuite de multiplier la puissance par le coefficient.

Ci-dessous, un graphique démontrant bien que la puissance d'un radiateur n'est pas proportionnelle au débit. A partir d'une chute de 6°C (calcul effectué avec une température de départ de 75 °C), la courbe s'aplatie fortement, démontrant qu'il est inutile d'utiliser une chute trop faible car le gain de puissance est insignifiant par rapport aux pertes de charge engendrées.
La chute de température peut être librement choisie entre 5 et 30°C mais afin de ne pas utiliser une chute trop faible qui n'apporterait que très peu de puissance supplémentaire, il est possible dans ce cas de vérifier l'efficacité thermique du radiateur. Cette efficacité ne devant pas être inférieure à 0,1 :
efficacité thermique = (Td - Tr) / (Td - Ti), avec Td = 90°C et Ti = 20°C la chute minimale qu'il est possible d'utiliser est de 7 °C : (90 - 83) / (90 - 20) = 0,1. Avec Td = 75 °C et Ti = 20 °C la chute minimale est de 6 °C.



Précision sur les débits.
La puissance d'un radiateur n'est pas proportionnelle au débit (graphique ci-dessus), c'est à dire que si on réduit de 50% le débit, on ne réduit pas la puissance du radiateur d'autant. Exemple :
Coefficient H de la pièce = 43 W/K
Température extérieure de base Te = -15°C
Température intérieure souhaitée dans la pièce Ti = 20°C
Déperditions thermique dans les conditions extérieures de base :
Dep = 43 x (20 - -15) = 1505 W
Débit nécessaire avec une chute de 10°C :
1505 / (10 x 1,1628) = 129,43 l/h
Admettons maintenant une erreur de débit de 20% en moins par rapport au débit nécessaire :
129,43 x 0,8 = 103,54
La chute avec ce débit n'est plus de 10°C mais de :
DeltaT = 1505 / (103,54 x 1,1628) = 12,5 °C
Température de retour :
Tr = 75 - 12,5 = 62,5 °C
Dans ces conditions, la puissance passe de 1505 W à :
Q = 1505 x (((75 - 62,5) / ln((75 - 20) / (62,5 - 20))) / 50)1,287 = 1446,44 W
Pourcentage de perte de puissance :
(1 - (1446,44 / 1505)) x 100 = 3,89%
On peut, à ce moment là, se poser la question suivante, "est il vraiment nécessaire d'être précis dans le réglage des débits puisque 20% de débit en moins ne génère que 3,89% de perte de puissance thermique ?" dans ce cas, voyons quelle sera la température d'équilibre thermique dans la pièce :
Ti = 1446,44 / 43 + -15 = 18,63 °C
La température qui règnera dans la pièce dans les conditions extérieures de base sera, non pas de 20 °C mais de 18,63 °C. On peut maintenant se poser une deuxième question, "est il possible de se contenter d'une température de confort de 18,63 °C au lieu des 20 °C souhaités ?" si non, comment faire pour obtenir les 20 °C sans toucher au débit ? en jouant sur la température de l'eau mais dans notre exemple, la température de départ est déjà de 75 °C, température qui est, pour les chaudières actuelles, la température maximale qu'elles peuvent atteindre (on peut débrider certains aquastats pour passer à 90 °C).
On peut donc en déduire que pour avoir la température souhaitée, il faut avoir le bon débit.
Maintenant, admettons le cas inverse, le débit est plus important de 20% :
129,43 x 1,2 = 155,3 l/h
chute avec ce débit :
DeltaT = 1505 / (155,3 x 1,1628) = 8,3 °C
Température de retour :
Tr = 75 - 8,3 = 66,7 °C
nouvelle puissance :
Q = 1505 x (((75 - 66,7) / ln((75 - 20) / (66,7 - 20))) / 50)1,287 = 1533,6 W
Pourcentage de gain de puissance :
((1533,6 / 1505) - 1) x 100 = 1,9%
Température d'équilibre thermique :
Ti = 1533,6 / 43 + -15 = 20,66 °C
Ceci démontre qu'il vaut mieux avoir un débit légèrement supérieur (légèrement, car les pertes de charge seront plus importantes) plutôt qu'inférieur.
 
puce Mise en oeuvre.
 
puce Définition du nombre d'éléments.
Pour définir le nombre d'éléments d'un radiateur, il faut connaître 5 paramètres :
- Déperditions calorifiques de la pièce.
- Température souhaité dans la pièce.
- Le DeltaT (différence de température entre l'eau du radiateur et l'air ambiant)
- Puissance par élément en W en fonction du DeltaT (il faut pour cela une documentation du fabricant)
- Température Départ/Retour chaudière (en général 75/65 °C) 
Exemple de calcul :
- Déperditions calorifiques de la pièce => 1350 W
- Température désirée dans la pièce => 20 °C
- Delta T => ((75 + 65) / 2) - 20 = 50 °C
- Puissance à l'élément => 119 W (donnée prise sur la documentation technique d'un fabricant. certain indiquent les puissances à différents DeltaT mais généralement à 50 °C)
donc nombre d'éléments = 1350 W / 119 W = 11,34 donc 12 éléments.
puce La pose.
La pose des radiateurs ne doit pas se faire n'importe comment. Il faut réfléchir à leur implantation. Les radiateurs se posent en règle générale sous ou à coté des ouvertures, qui elles ont la plus grande déperdition calorifique.
Note : le fait de mettre un radiateur sous une fenêtre ou sur un mur extérieur augmente les déperditions thermiques au dos de l'émetteur car elles sont fonction de l'écart moyen des températures intérieure/extérieure ce qui, bien sûr, réduit le rendement de l'installation. Seulement, sous une fenêtre il réduit le rayonnement froid du vitrage bien qu'avec les nouveaux produit ceci soit moins flagrant.
L'esthétique est aussi très importante, si un radiateur est posé sous une fenêtre, veiller à le centrer bien dans l'axe de celle-ci. Si il est placé sur un mur, réfléchir à l'ameublement. Si la pièce va recevoir 2 radiateurs, penser à la symétrie. Positionner le radiateur et prendre du recul pour en voir l'effet, le fait de le déplacer de quelques dizaines de centimètres par rapport à son emplacement logique ne nuira pas à son efficacité. Ne pas déshabiller les radiateurs de leurs emballage de protection jusqu'à la finition des travaux ou la mise en chauffe. Faire des découpes pour l'emplacement des consoles et des raccordements. En ce qui concerne la distance par rapport au sol, il est conseillé de ne pas descendre au dessous de 10 cm, ceci pour une bonne convection ainsi que pour l'esthétique et le nettoyage (passage du balai). La distance "standard" appliqué par la majorité des installateurs est de 15 cm et 20 à 25 cm pour les panneaux à raccordement par le bas. Veiller, si la pose des radiateurs se fait avant la chape, à rajouter à la mesure l'épaisseur de celle-ci.
L'accrochage aux murs des radiateurs se fait à l'aide de consoles adaptées au modèle du radiateur. Elles sont en général livrées avec. Les consoles livrées sont à visser. Il y a 2 sortes de consoles à visser. Les consoles à accrochage haut et bas (monobloc), en général 2 suffisent par radiateur selon le support et les consoles individuelles, dans ce cas 4 par radiateur vous seront nécessaire et là aussi selon le support.
Pour la prise des mesures, le plus simple est de coucher le radiateur face avant vers le sol et d'accrocher les consoles sur les barres appropriées, placer le mètre sur le radiateur en alignement des consoles de façon à se qu'il dépasse du bas du radiateur de la distance par rapport au sol, en général 15 cm, puis viser la mesure à hauteur du 1er trou de la console monobloc ou de la console basse et la reporter au mur, faire de même pour le trou ou la console du haut. Pour les radiateurs lamellaires ou à éléments démontables les consoles se posent, en général, entre le 4ème et  5ème élément en partant du bord. Pour les radiateurs rideaux en acier des pattes pliées et soudées sont prévu à cet effet, il n'y a qu'à les centrer dessus. Pour les consoles à pliage à 90° faire attention au décalage d'axe qui est, d'une manière générale, de 12 à 17 mm vers la droite ou vers la gauche selon le sens de pliage. Penser donc à décaler vers la gauche ou vers la droite l'axe des percements par rapport à l'axe de la console sinon le radiateur ne sera pas centré.
Les radiateurs doivent être posés de niveau, il ne sert à rien de mettre une pente vers la purge car le flux de l'eau pousse l'air vers le purgeur.
Pour l'utilisation des consoles à sceller (radiateur trop lourd) la prise des mesures est la même que pour les consoles à visser. Pour les percements, tracer les axes verticaux et horizontaux d'une longueur minimale de 20 cm de manière à ne pas les effacer lors du percement. Faire des trous carrés de 8 cm de coté avec un évasement vers l'intérieur, poser une règle de niveau tenue par des chevillettes sur les percements hauts, faire correspondre le haut de la règle au bas des consoles, mouiller les trous puis remplir de mortier de scellement ou de plâtre, enfoncer les consoles bien dans l'axe et de niveau, bourrer à nouveau de mortier ou de plâtre, laisser tirer. Procéder de la même façon pour les consoles du bas. Faire bien attention à la profondeur de scellement des consoles ; un petit trait de scie est conseillé. Le radiateur doit être à environ 3 à 4 cm du mur, donc pour prendre la mesure accrocher la console au radiateur, tracer l'arrière du radiateur sur la console, rajouter 3 à 4 cm et faire une marque à la scie à métaux.
puce Le raccordement.
Pour le raccordement des radiateurs les tuyaux peuvent être apparents ou encastrés. Le robinet est à placer, si possible, du coté de l'arrivée de l'eau en provenance de la chaudière. Il y a différentes façon des les raccorder.
puce Le robinet et le coude ou té de réglage du même coté, ceci jusqu'à ce que la longueur du radiateur ne dépasse pas 2 fois sa hauteur, exemple: jusqu'à 1,20 m de long pour une hauteur de 0,60 m.
puce Le robinet et le coude ou té de réglage à l'opposé l'un de l'autre quand la longueur du radiateur dépasse 2 fois sa hauteur.
puce Le robinet et le coude ou té de réglage au bas du radiateur (en règle générale, pour les panneaux). Faire très attention pour le raccordement des panneaux car ils ont un sens. Certains ont des étiquettes mais d'autre n'ont rien. Il faut regarder si un petit emboutissage se trouve sur une des parties horizontales. Les branchements doivent se faire du coté ou il y a cet emboutissage.
puce Le robinet et le coude ou té de réglage en haut (en règle générale, pour les panneaux).
puce A l'aide d'un robinet à trois ou quatre voies. Utilisé quand l'alimentation se fait par des tuyaux venant de la chape (cuivre ou retube). 
puce Pose des accessoires.
puce Robinet à tête mécanique. La position d'installation importe peu, tête vers le haut, vers le coté ou vers l'avant. Il n'y a aucun problème pour un bon fonctionnement.
puce Robinet à tête thermostatique. Pour ce modèle, il en va tout autrement car il ne doit pas être positionné la tête vers le haut mise à part avec une tête à bulbe à distance ou une commande à distance car sinon la chaleur émise par le tuyau influencerait son bon fonctionnement. Il ne doit pas être non plus derrière des rideaux épais car ils confinent la chaleur autour de la tête et fausse par la même son bon fonctionnement.
puce Le Coude et Té de réglage. Leur positionnement se fait toujours sur le retour du radiateur. Comme leur noms l'indiquent ils servent au réglage donc à l'équilibrage du circuit de chauffage. On dit Coude de réglage car il permet un changement de direction de 90° par rapport à la sortie du radiateur, le Té de réglage par contre permet une sortie dans l'alignement de celle du radiateur. Le réglage de ces organes ce fait toujours en partant de la position fermée et en comptant le nombre de tours d'ouverture.
puce

Vissage des accessoires.
Une clé appropriée est nécessaire pour le vissage des robinets et coudes ou tés de réglages. Clé qu'on peut se procurer facilement auprès de magasins spécialisés pour un coût assez modique.
Démonter la douille filetée et l'écrou, laisser ce dernier sur la douille puis l'enfiler sur l'outil de montage, mettre celui-ci dans l'étau en position horizontale et du coté droit, faire le joint puis effectuer le vissage en tournant dans le sens horaire. Ceci fait, à l'aide d'une lame de scie à métaux et en faisant attention de ne pas rayer le radiateur éliminer l'excédent de filasse qui a été repoussé.

 

puce

Calcul des pertes de charge.
 

puce

La hauteur manométrique.(H.M.)
Tout fluide mis en mouvement dans une conduite résulte d'une charge ou pression, quelle soit donnée par un circulateur ou en thermosiphon par la différence de densité entre l'eau chaude et l'eau froide. Tout au long du circuit cette charge subit une usure que l'on appelle "Perte de charge".
Les pertes de charge sont dues d'une part au frottement du fluide contre les parois de la conduite que l'on appelle "Pertes de charge linéiques" caractérisées par la lettre J et d'autre part au passage des différentes singularités jalonnant le circuit (coudes, tés, vannes, robinets, chaudière, radiateurs, etc...) que l'on appelle "Pertes de charge singulières" caractérisées par la lettre Z. Les pertes de charge (DeltaP)  se mesurent en différentes unités : en Pa (Pascal), en daPa (déca Pascal), en bar, en mbar (millibar), en mmCE ou mCE (millimètre ou mètre de colonne d'eau). La profession utilise généralement le daPa, le mmCE ou le mCE. Dans le site, et plus particulièrement ici, j'utilise le mmCE donc la colonne d'eau en millimètre, colonne que l'on appelle hauteur manométrique. Le calcul des pertes de charge demande du travail et n'est pas chose aisée. Je vais donc essayer d'être le plus clair possible.
Ci dessous un tableau de conversion de valeurs :
 

  Pa daPa bar mbar mCE mmCE
Pa - 0,1 0,00001 0,01 0,00010193 0,10193
daPa 10 - 0,0001 0,1 0,0010193 1,0193
bar 100000 10000 - 0,001 10,193 10193
mbar 100 10 0,001 - 0,010193 10,193
mCE 9810 981 0,0981 98,1 - 1000
mmCE 9,81 0,981 0,0000981 0,0981 0,001 -


Il est possible d'utiliser 2 méthodes pour définir J et Z.

puce

1ère méthode
Dans cette 1ère méthode on a 2 façons de procéder.
- 1ère façon. Calculer la longueur totale départ et retour du circuit le plus défavorisé (en général le circuit alimentant le radiateur le plus éloigné de la chaudière) celui qui aura donc la HM la plus élevée, adopter une valeur moyenne pour J de 10 à 20 mmCE/m (10 à 20 millimètres de colonne d'eau par mètre de conduite) de pertes de charge linéiques et prendre un rapport J/Z de 55/45. 55% de pertes par frottement et 45% de pertes singulières (ce rapport est défini de façon arbitraire et est fonction de la configuration de l'installation). Exemple :
Longueur de circuit Départ Retour 38m
38 x 15 = 570 mmCE de pertes par frottement.
570 x (0,45 / 0,55) = 466,37 mmCE de pertes singulières (ici rapport Z/J, rapport J/Z : 570 / (0,55 / 0,45) = 466,37 mmCE).
HM du circuit 570 + 466,37 = 1036,37 mmCE ou 1,03637 mCE.
Cette perte de charge est celle qui va servir de base pour le calcul des diamètres avec les débits correspondants à chaque tronçons et à l'aide du tableau A pour le cuivre et le Per et le tableau B pour l'acier (Les valeurs des tableaux ont étés obtenues avec une température de départ du fluide de 55°C et un DeltaT de 10°C). Pour la recherche des diamètres (utiliser la ligne 15 et rechercher le débit égal ou immédiatement supérieur à celui du tronçon étudié et lire en tête de colonne le diamètre correspondant). On appelle cette perte de charge, la perte de charge de base ou la perte de charge de référence.
Cette HM sera l'un des 2 paramètres pour définir le choix du circulateur (l'autre étant le débit total de l'installation). Avec cette façon on part de J pour trouver la HM.
- 2ème façon. Partir d'une HM définie comme c'est le cas pour une chaudière murale ou au sol dans laquelle le constructeur a déjà installé le circulateur (voir plus bas 1er exemple de calcul). Exemple :
HM 1100 mmCE
Longueur du circuit Départ Retour 38m
J = 1100 x 0,55 / 38 = 15,92 mmCE/m (valeur moyenne)
Z = 1100 x 0,45 = 495 mmCE
Il est possible de ramener Z en mmCE/m pour faciliter les calculs (valeur moyenne).
495 / 38 = 13,02 mmCE/m. Avec cette façon on part d'une HM pour trouver J et Z. Pour définir les diamètres des différents tronçons, utiliser les tableaux A ou B et (pour l'exemple) à la ligne 16 (valeur immédiatement supérieure à 15,92), chercher le débit égal ou immédiatement supérieur à celui du tronçon étudié et lire en tête de colonne le diamètre correspondant. Si dans le cas où la valeur de J serait supérieure à 20 mmCE/m (valeur maximale conseillée), ceci indiquerait que la HM disponible est trop importante et dans ce cas, il y aurait lieu de créer une perte de charge artificielle à l'aide d'un organe de réglage installé sur la conduite de retour (ou départ) chaudière ou à l'aide des coudes ou tés de réglage des radiateurs.
Dans l'exemple où la HM disponible serait de 2500 mmCE, avec une longueur de 38m :
J = (2500 x 0,55) / 38 = 36,18 mmCE/m, ce qui donne une valeur pour J trop importante, il faudra alors créer une perte de charge artificielle de façon à éviter les vitesses excessives et donc une suralimentation des radiateurs ce qui induirai une chute plus faible et une puissance de ceux ci non conforme aux calculs. Pour avoir une base de départ la HM pourra être définie de façon arbitraire ou en adoptant une valeur pour J ce situant entre 10 et 20 mmCE/m. Avec une valeur proche de 10 mmCE/m les conduites auront un diamètre plus important mais des vitesses de fluide plus basses, il faudra donc la définir dans un juste milieu, des diamètres pas trop faibles pour ne pas avoir des vitesses de fluide trop importantes et donc des risques de bruit mais malgré tout des diamètres pas trop importants afin de limiter le prix de revient de l'installation ainsi que les pertes thermiques des conduites, pertes qui sont proportionnelles à la surface.
J = 18 mmCE/m, (18 + (18 x (0,45 / 0,55))) x 38 = 1243,64, la perte de charge artificielle sera de 2500 - 1243,64 = 1256,36 mmCE. La perte de charge qui va servir de base aux calculs (perte de charge de référence) sera de 1243,64 mmCE mais si sa valeur ne suffit pas et demandera donc l'emploi de diamètres plus importants il est tout à fait possible de l'augmenter (les calculs effectués seront à reprendre avec la nouvelle valeur).
Il est aussi possible de débuter les calculs en gardant comme perte de charge de référence celle du circulateur (exemple 2500 mmCE), les pertes de charge artificielles seront définies au long des calculs mais dans ce cas faire attention car la perte de charge disponible sera généralement assez importante et on aura le réflexe de toujours prendre un diamètre inférieur ce qui induira des vitesses de fluide plus importantes et des risques de bruits (sifflements).
puce

2ème méthode.
Cette méthode est plus complexe et demande la connaissance parfaite du cheminement des conduites, du nombre de raccords utilisés ainsi que leur forme, du rayon de courbure des coudes, etc... Il faut pour celle-ci utiliser les formules et tableaux de la page "Formules/Tableaux". Un exemple est utilisé pour que ce soit plus facile à comprendre (voir plus bas 2ème exemple de calcul). Un classeur Excel est disponible en téléchargement "Pertes de charge.xls" afin de facilité les différents calculs pour l'utilisation de cette méthode.
 
puce

précision sur les Circuits et tronçons.
- Circuit :
On appelle un circuit, la longueur complète des conduites alimentant un radiateur en partant de la chaudière, ce circuit peut avoir des conduites de différents diamètres qui sont les tronçons. Il y a le circuit principal qui est généralement celui du radiateur le plus défavorisé et les circuits dérivés qui alimentent les autres radiateurs.
- Tronçon :
On appelle un tronçon, une partie du circuit allant d'un raccordement à un autre comme par exemple entre 2 tés qui alimentent chacun un radiateur, un circuit dérivé ou encore de la chaudière au 1er té rencontré.
 
puce

Définition des diamètres pour radiateurs.

- 1er exemple :
 Pour expliquer la façon de procéder, nous allons prendre un exemple et utiliser un croquis afin d'être plus facile à comprendre. Il faut savoir que pour définir les diamètres des conduites à utiliser un certain nombre de données seront nécessaires.
- Déperditions calorifiques de chaque pièces afin de connaître la puissance de chaque radiateur.
- Dimensionnement et implantation des radiateurs.
- Cheminement des conduites (surtout leurs longueurs).
- HM de référence du circulateur.
Pour cet exemple, nous prendrons une chaudière munie d'un circulateur Grundfos UPS 25-40 180. Le circulateur est, dans ce cas, imposé.
Caractéristiques du circulateur :
3 vitesses manuelles.
1ère vitesse, HM à débit nul de 2,4 mCE, débit à HM nulle de 2200 l/h. Plage optimale d'utilisation : HM de 1,5 mCE pour un débit de 500 l/h à une HM de 0,5 mCE pour un débit de 1500 l/h.
2ème vitesse, HM à débit nul de 3,5 mCE, débit à HM nulle de 3000 l/h. Plage optimale d'utilisation : HM de 2,7 mCE pour un débit de 600 l/h à une HM de 0,7 mCE pour un débit de 2250 l/h.
3ème vitesse, HM à débit nul de 4 mCE, débit à HM nulle de 3600 l/h. Plage optimale d'utilisation : HM de 3,3 mCE pour un débit de 700 l/h à une HM de 0,8 mCE pour un débit de 2900 l/h.
Dans le cadre de l'exemple, l'installation a un débit total de 614 l/h. Aux vues des performances du circulateur et du débit total de l'installation, le choix va porter sur la vitesse 1 et nous prendrons une HM de 1 mCE (1000 mmCE). Pour plus de précision, il faudrait la définir en fonction du débit par rapport à la courbe de puissance sur l'abaque pour la vitesse choisie. Dans l'exemple, pour un débit de 614 l/h sur la courbe de la vitesse 1 la HM correspondante est de 1250 mmCE. A été choisie une HM inférieure tout simplement pour avoir une petite marge de manoeuvre (avec une HM plus faible les diamètres des conduites devrons être plus forts) car le jour de l'exécution des travaux, on rencontre parfois des imprévus qui font que les conduites ne passent pas toujours comme défini sur le plan et leurs longueurs peuvent changer et souvent en augmentant ce qui entraînera donc une augmentation des pertes de charge et dans ce cas ci, elles seront absorbées par la marge supplémentaire (un calcul devra bien évidemment être refait afin de connaître les pertes de charge artificielles à créer). En ne tenant pas compte de cette éventualité et en définissant la HM de façon précise si le cheminement des conduites du circuit le plus défavorisé est modifié et donc les pertes de charges augmentées, il se peut que le dernier radiateur ne reçoive pas le débit d'eau qui lui est nécessaire et il ne développera donc pas la puissance voulue. Ceci obligera alors le passage en 2ème vitesse et s'ensuivra un déséquilibre de toute l'installation. Par contre, si il advenait que le cheminement des conduites soit conforme aux prévisions, il suffira de créer une petite perte de charge artificielle supplémentaire (qui sera à rajouter à celle déjà nécessaire) afin de réduire l'excédant de débit.
Pour l'exemple, nous allons adopter un rapport J/Z de 55/45%. Les résultats sont systématiquement arrondis à la valeur supérieure pour la 2ème décimale.
Pour cet exemple, la nature des conduites est du cuivre donc valeur en Tableau A.
 

puce

Circuit le plus défavorisé.
Dans un premier temps, définir le circuit le plus défavorisé et totaliser sa longueur départ retour.
Sur le croquis, le circuit le plus défavorisé est le circuit alimentant le radiateur R5.
- Calcul de la longueur du circuit Départ ABCDE et Retour E'D'C'B'A'.
1 + 5,5 + 1,25 + 8,7 + 6,3 + 0,8 + 0,2 + 6,3 + 8,7 + 0,75 + 5,85 + 1,5 + 0,5 = 47,35m
Calcul de la valeur moyenne de J en mmCE/m.
(1000 x 0,55) / 47,35 = 11,62 (pertes par frottement)
- Calcul de la valeur moyenne de Z en mmCE/m.
(1000 x 0,45) / 47,35 = 9,51 mmCE/m (pertes singulières)
Précision sur les valeurs de J.
Afin d'éviter les risques de bruits dus à une vitesse excessive du fluide, il est bon de ne pas dépasser, dans la mesure du possible, une valeur de 20 mmCE/m. Une valeur trop basse entraîne aussi des diamètres de conduite plus fort. Une plage entre 5 et 20 mmCE/m est acceptable pour J mais si pour ne pas dépasser la HM disponible une valeur pour J doit être inférieure à 5 mmCE/m ceci n'est pas un problème. Par contre, si pour éviter de devoir installer dans un tronçon une conduite d'un diamètre trop important il est nécessaire de dépasser la valeur de 20 mmCE/m ceci n'est pas non plus un problème seulement, dans ce cas, il faudra faire attention à ne pas dépasser une vitesse du fluide de 0,80 à 0,85 m/s. Dans tous les cas, éviter de dépasser la valeur de 25 mmCE/m. Dans les tableaux A et B, les valeurs entre parenthèses sont les vitesses du fluide en m/s.
- Calcul du débit total.
Il faut savoir que les conduites alimentant les radiateurs ont une émission thermique non négligeable. Émission qui doit donc être prise en compte dans le calcul des débits afin d'avoir au radiateur le débit d'équilibre thermique. Ces émissions sont fonction de plusieurs paramètres comme le DeltaT entre la température de la conduite et celle de l'air ambiant, si elle est isolée ou non, du diamètre de celle-ci. Le calcul étant assez complexe il est courrant de prendre comme valeur 20% qui seront rajoutés à la puissance de chaque radiateur. Si malgré tout les émissions thermiques réelles doivent être connues, la méthode de calcul est expliquée à la page "Formules/Tableaux". Pour calculer le débit en litres/heure, utiliser la formule, Q / (DeltaT x 1.1627 x p)
Q = puissance en Watts
DeltaT est la différence (chute de température) entre le départ et retour chaudière qui est de 15°C valeur communément admise pour les radiateurs (la chute de 10°C est la valeur normalisée mais elle induit des débits plus importants). Dans le cadre de l'exemple, une chute de 15°C commune à tous les radiateurs sera adoptée.
p est la densité du fluide en fonction de sa température en kg/l. 70°C étant la température moyenne admise pour un circuit radiateur quand on atteint à l'extérieur la température de base (voir à la page "Température de base"), la densité de l'eau à cette température est de 0,9777 kg/l. (pour d'autres T°, voir le tableau sur la page "Formules/Tableaux")
Pour simplifier les calculs, il est possible d'utiliser un coefficient : Ce = 1 / (15 x 1.1627 x 0,9777) = 0,05864
Débit des différents radiateurs :
R1 = 3000 x Ce = 175,92
R2 = 1100 x Ce = 64,50
R3 = 2350 x Ce = 137,80
R4 = 750 x Ce = 43,98
R5 = 1500 x Ce = 87,96
Le débit effectif de chaque radiateur est son débit propre + les 20% dus aux émissions thermiques des conduites le raccordant.
R1 = 175,92 x 1.20 = 211,1 arrondi à 211 l/h
R2 = 64,50 x 1.20 =77,4 arrondi à 78 l/h
R3 = 137,80 x 1.20 = 165,36 arrondi à 166 l/h
R4 = 43,98 x 1.20 = 52,77 arrondi à 53 l/h
R5 = 87,96 x 1.20 = 105,55 arrondi à 106 l/h

puce

Diamètres pour le circuit le plus défavorisé. (circuit principal)
A l'aide du tableau A prendre la ligne correspondante à la valeur moyenne de J ou celle immédiatement supérieure et chercher dans cette ligne le débit d'eau en l/h égal ou immédiatement supérieur. En regard de ce débit, lire en tête de colonne le diamètre à utiliser.
A ce stade, 2 façons peuvent être utilisées. L'une simplifiée mais plus approximative et l'autre un peu plus complexe mais plus précise quand aux pertes de charge des différents tronçons.
- Façon simplifiée.
J = 11,62 donc 12 mmCE/m
entre parenthèse les débits immédiatement supérieurs du tableau A.
tronçons AB B'A' 614 (953) diamètre 26x28
tronçons BC C'B' 614 - 211 - 78 = 325 (468) diamètre 20x22
tronçons CD D'C' 325 - 166 = 159 (177) diamètre 14x16
tronçons DE E'D' 159 - 53 = 106 (116) diamètre 12x14
Il est aussi possible d'adopter cette façon pour calculer les tronçons alimentant le circuit dérivé.
tronçons BF F'B' 211 + 78 = 289 (468) diamètre 20x22
tronçons FG G'F' 289 - 211 = 78 (116) diamètre 12x14
- Façon plus complexe.
Il est plus facile pour cette façon de commencer par les tronçons de bout de circuit mais ce n'est pas une obligation. Il faut savoir que le calcul des diamètres ne se fera pas toujours en une seule passe, ceci veut dire qu'il est possible qu'une valeur choisie pour J dans un tronçon soit probablement à revoir si, pour les tronçons suivants, la HM disponible est trop faible et oblige donc l'emploi de plus gros diamètres afin de ne pas dépasser la perte de charge de référence. Il est conseillé de ne pas utiliser de valeurs pour J trop importantes en fin de circuit (coté dernier radiateur) car elles entraîneront probablement l'emploi de diamètres plus fort en début de circuit (coté chaudière) et donc ceci augmentera le coût de l'installation (plus élevée sera la perte de charge en bout de circuit, plus fort seront les diamètres en début de circuit). La différence de prix est plus importante entre les diamètres 20x22 et 26x28 qu'elle ne l'est entre les diamètres 12x14 et 14x16. Il est prudent de ne pas dépasser une valeur de 10 mmCE/m pour le ou les tronçons de bout de circuit, par contre pour les tronçons de début de circuit la valeur de J pourra être supérieure à 10 afin de réduire si possible les diamètres et donc le prix de revient.
puce

Diamètre pour les tronçons DE E'D'
On va prendre pour base de départ la valeur pour J de 10mmCE/m.
Débit des tronçons : R5 = 106 l/h
A la ligne 10, un débit de 106 l/h donne un débit immédiatement supérieur de 159 l/h pour un diamètre de 14x16. Avec un écart de 53 l/h il est facile d'en déduire que la perte de charge linéique (par frottement) sera inférieure à 10 mmCE/m, bien que la perte de charge ne soit pas proportionnelle au débit du fluide. On va donc descendre dans les débits de la colonne 14x16 afin de trouver le débit égal ou immédiatement supérieur à 106 l/h. On trouve 106 l/h mais pour ce débit, la valeur de J n'est plus que de 5 mmCE/m et ici commence la gymnastique entre les débits et les valeurs de J afin d'avoir le diamètre le mieux adapté et une perte de charge correcte afin d'éviter les risques de bruit du circulateur et des conduites. En partant de cette nouvelle valeur moyenne pour J on va définir celle de Z et ainsi les pertes de charge par frottement et singulières.
- Valeur moyenne de J
5 mmCE/m
- Valeur moyenne de Z
Z = 5 x (0,45 / 0,55) = 4,10 mmCE/m
- Pertes de charge par frottement
DE = 7,1 x J (5) = 35,50 mmCE
E'D' = 6,5 x J = 32,50 mmCE
- Pertes de charge singulières
DE = 7,1 x Z (4,10) = 29,11 mmCE
E'D' = 6,5 x Z = 26,65 mmCE
- Pertes de charge totales
35,50 + 32,50 + 29,11 + 26,65 = 123,76 mmCE pour un diamètre de 14x16
puce

Diamètre pour les tronçons CD D'C'
Pour définir le diamètre de ces tronçons, il faut connaître la perte de charge disponible. On va donc déduire à la perte de charge de base (1000 mmCE) la perte de charge des tronçons précédents.
- Perte de charge disponible
1000 - 123,76 = 876,24 mmCE
- Valeur moyenne de J pour cette perte de charge
J = (876,24 x 0,55) / (8,70 + 8,70) = 27,69 mmCE/m
Débit des tronçons : R4 + R5 =  53 + 106 = 159 l/h
J = 27,69 donc 28 mmCE/m
Ici la valeur de J est trop importante car elle est en dehors de la plage conseillée (maxi 20 mmCE/m). Par mesure de prudence et comme on est encore pour ainsi dire en bout de circuit, on va prendre comme valeur de départ les 10 mmCE/m afin de ne pas risquer de créer une perte de charge trop forte et de devoir ensuite prendre, en début de circuit, un diamètre plus important qu'il ne serait nécessaire. A la ligne 10, le débit de 159 l/h donne un débit de 159 l/h pour un diamètre de 14x16. L'écart de débit étant nul, la perte de charge moyenne pour J sera de 10 mmCE/m.
- Valeur moyenne de J
10 mmCE/m
- Valeur moyenne de Z
Z = 10 x (0,45 / 0,55) = 8,19 mmCE/m
- Pertes de charge par frottement
CD = 8,7 x J (10 ) = 87 mmCE
D'C' = 8,7 x J = 87 mmCE
- Pertes de charge singulières
CD = 8,7 x Z (8,19) = 71,26 mmCE
D'C' = 8,7 x Z =  71,26 mmCE
- Pertes de charge totales
(87 x 2) + (71,26 x 2) = 316,52 mmCE pour un diamètre de 14x16
puce

Diamètre pour les tronçons BC C'B'
- Perte de charge disponible
1000 - 123,76 - 316,52 = 559,72 mmCE
- Valeur moyenne de J pour cette perte de charge
J = (559,72 x 0,55) / (5,5 + 1,25 + 0,75 + 5,85) = 23,06 mmCE/m
Débit des tronçons : R3 + R4 + R5 = 166 + 53 + 106 = 325 l/h
J = 23,06 donc 24
A cet endroit du circuit on ne va plus prendre en compte la valeur limite de bout de circuit (10 mmCE/m) afin de ne pas avoir de diamètre trop important. On va utiliser la valeur moyenne de J qui est de 24 mmCE/m. Cette valeur est trop importante car elle se situe en dehors de la plage conseillée (maxi 20 mmCE/m) mais malgré tout on va partir de cette valeur pour voir si dans la colonne du débit égal ou immédiatement supérieur à 325 l/h il est possible de redéfinir la valeur de J pour qu'elle soit acceptable c'est à dire en dessous de 20 mmCE/m. A la ligne 24, 325 l/h donne un débit immédiatement supérieur de 379 l/h pour un diamètre de 16x18. L'écart de débit étant de 54 l/h, on va donc descendre dans les débits de la colonne 16x18 pour redéfinir J. On trouve le débit de 332 l/h et la valeur de J est 19 mmCE/m.
- Valeur moyenne de J
19 mmCE/m
- Valeur moyenne de Z
Z = 19 x (0,45 / 0,55) = 15,55 mmCE/m
- Pertes de charge par frottement
BC = 6,75 x J (19) = 128,25 mmCE
C'B' = 6,60 x J = 125,40 mmCE
- Pertes de charge singulières
BC = 6,75 x Z (15,55) = 120,52 mmCE
C'B' = 6,60 x Z =  102,63 mmCE
- Pertes de charge totales
128,25 + 125,40 + 120,52 + 102,63 = 476,80 mmCE pour un diamètre de 16x18
puce

Diamètre pour les tronçons AB B'A'
- Perte de charge disponible
1000 - 123,76 - 316,52 - 476,80 = 82,92 mmCE
- Valeur moyenne de J pour cette perte de charge
J = (82,92 x 0,55) / (1 + 1,5 + 0,50) = 15,21 mmCE/m
Débit des tronçons : R1 + R2 + R3 + R4 + R5 = 211 + 78 + 166 + 53 + 106 = 614 l/h
J = 15,21 donc 16
A la ligne 16, 614 l/h donne un débit immédiatement supérieur de 1122 l/h pour un diamètre de 26x28. L'écart de débit est de 508 l/h. En descendant dans les débits de la colonne 26x28, le débit immédiatement supérieur est 642 l/h pour une valeur de J de 6 mmCE/m.
- Valeur moyenne de J
6 mmCE/m
- Valeur moyenne de Z
Z = 6 x (0,45 / 0,55) = 4,91 mmCE/m
- Pertes de charge par frottement
AB = 1 x J (6) = 6 mmCE
B'A' = 2 x J = 12 mmCE
- Pertes de charge singulières
AB = 1 x Z (4,91) = 4,91 mmCE
B'A' = 2 x Z =  9,82 mmCE
- Pertes de charge totales
6 + 12 + 4,91 + 9,82 = 32,73 mmCE pour un diamètre de 26x28
Perte de charge totale du circuit le plus défavorisé s'élève à : 123,76 + 316,52 + 476,80 + 32,76 = 949,68 mmCE pour une perte de charge disponible de 1000 mmCE.
A ce stade des calculs, les diamètres à utiliser pour le circuit le plus défavorisé sont :
DE E'D' = 14x16
CD D'C' = 14x16
BC C'B' = 16x18
AB B'A' = 26x28
Dans ce cas, on s'aperçoit que les tronçons AB B'A' ont un diamètre assez important par rapport aux autres mais ici et dans ces conditions, il n'est pas possible de réduire leurs diamètre car la perte de charge résultante (1000 - 949,68 = 50,32 mmCE) ne permet pas d'utiliser le diamètre inférieur (20x22) car dans ce cas la perte de charge disponible serait dépassée (1000 - 1026,19 = -26,19 mmCE) et il en résultera une sous alimentation du radiateur le plus défavorisé. Si on veut réduire le diamètre de ces tronçons, il va falloir augmenter le diamètre d'autres tronçons.
Les questions qu'il faut alors se poser sont : est ce que, pour l'esthétique, il vaut mieux avoir un diamètre plus petit en bout et milieu de circuit, vu que ces conduites se trouveront probablement dans une pièce à vivre (salon, salle à manger, etc...) et avoir un diamètre plus fort en début de circuit où les conduites se situeront plutôt dans le garage ou la chaufferie et ceci au détriment du prix de revient de l'installation ? ou alors, pour réduire le coût mais bien sûr au détriment de l'esthétique, augmenter le diamètre en bout ou milieu de circuit afin de réduire le diamètre des tronçons de début de circuit ? Dans l'exemple, optons pour la 2ème alternative c'est à dire réduire le coût de l'installation en réduisant le diamètre des tronçons AB B'A'. Il faut donc choisir les tronçons pour qui les diamètres vont augmenter. Portons le choix sur les avant derniers tronçons CD D'C' qui sont pour le moment en 14x16. En prenant le diamètre au dessus (16x18) et en partant du bas ou du haut de la colonne on va chercher le débit égal ou immédiatement supérieur à 159 l/h. On trouve le débit de 171 l/h avec une valeur pour J de 6 mmCE/m. En reprenant les calculs à partir de ces tronçons et avec la nouvelle valeur de J la perte de charge totale des tronçons CD D'C' est maintenant de 189,84 mmCE (au lieu de 316,52 mmCE). Perte de charge totale et diamètre pour les tronçons BC C'B' inchangés. Tronçon AB B'A', perte de charge maintenant disponible, 209,60 mmCE au lieu de 82,92 mmCE, valeur moyenne de J 38,32 mmCE/m, hors du tableau A, donc en partant de la colonne 10x12 et en remontant les débits on va chercher le débit égal ou immédiatement supérieur à 614 l/h sans toutes fois dépasser les 20 mmCE/m. On trouve le débit de 626 l/h dans la colonne 20x22 et une valeur pour J de 20 mmCE/m. Perte de charge totale pour les tronçons, 109,11 mmCE.
Les diamètres redéfinis, les différents calculs font ressortir que la perte de charge totale du circuit le plus défavorisé s'élève à : 123,76 + 189,84 + 476,80 + 109,11 = 899,51 mmCE pour une perte de charge disponible de 1000 mmCE, ce qui est un bon résultat car la perte de charge résultante n'est que de 100,49 mmCE. Pour cette perte de charge excédante, 2 solutions se présentent :
1ère solution, installer un organe d'équilibrage sur la conduite départ ou retour de la chaudière (tronçons AB ou B'A'), dans ce cas, pour les tronçons suivants (BF F'B' et les tronçons propres à chaque radiateur) la perte de charge de référence à prendre en compte sera non pas 1000 mmCE mais 899,51 mmCE.
2ème solution, utiliser les organes d'équilibrages de chaque radiateur (coudes ou tés de réglages) et ajouter la perte de charge excédante à chaque perte de charge artificielle déjà nécessaire, ce qui sera fait automatiquement en prenant en compte, comme perte de charge de référence, non pas 899,51 mmCE mais 1000 mmCE. Pour le radiateur le plus défavorisé (R5) une perte de charge artificielle sera à créer et devra être égale à la perte de charge excédante afin qu'il ne devienne pas le radiateur le plus favorisé une fois les pertes de charge artificielles créées sur les autres radiateurs et ceci pour qu'il est le débit d'équilibre thermique qui lui est nécessaire et lui seul (dans l'exemple, 106 l/h).
Tronçons AB B'A' perte de charge totale de 109,11 mmCE pour un diamètre de 20x22
Tronçons CD D'C' perte de charge totale de 189,84 mmCE pour un diamètre de 16x18
Pour la suite de l'exemple nous allons utiliser la 2ème solution donc prendre comme perte de charge de référence 1000 mmCE.
 

puce

Diamètre pour les tronçons BF F'B' (tronçons du circuit dérivé)
- Perte de charge disponible
1000 - 109,11 = 890,89 mmCE
- Valeur moyenne de J pour cette perte de charge
J = (890,89 x 0,55) / (1,45 + 1,20) = 184,91 mmCE/m
Débit des tronçons : R1 + R2 = 211 + 78 = 289 l/h
Avec une telle valeur on peut constater qu'on sort du cadre du tableau A. 184,91 mmCE/m induirait une telle vitesse que des bruits désagréables seraient générés car les diamètres qu'il faudrait utiliser seraient bien inférieurs à 10x12, diamètres qui ne sont jamais utilisés en chauffage pour alimenter un radiateur. On va donc remonter les colonnes des diamètres en commençant par la colonne 10x12 jusqu'à trouver le débit égal ou immédiatement supérieur à 289 l/h tout en étant inférieur à 20 mmCE/m. On trouve le débit de 290 l/h dans la colonne 16x18 avec une valeur pour J de 15 mmCE/m. Ici on serait tenté de prendre un diamètre au dessus afin d'avoir, pour J, une valeur inférieure (diamètre 20x22, débit 314 l/h, J = 6 mmCE/m) pour pouvoir réduire les diamètres en bout de circuit. Ce n'est pas utile car ce tronçon n'est pas le plus défavorisé et vu la perte de charge disponible (890,89 mmCE) les radiateurs raccordés sur ce tronçon (R1 et R2) auront forcément une perte de charge artificielle relativement importante et un organe d'équilibrage ne doit pas être trop fermé sinon il y a risque d'obstruction et parfois de bruit, ceci risque de limiter la perte de charge qu'il est capable de créer. Donc on va conserver la diamètre de 16x18 et la valeur de 15 mmCE/m pour J, de cette façon la perte de charge artificielle à créer sera moindre pour les 2 radiateurs car une partie sera absorbée par les conduites.
- Valeur moyenne de J
15 mmCE/m
- Valeur moyenne de Z
Z = 15 x (0,45 / 0,55) = 12,28 mmCE/m
- Pertes de charge par frottement
BF = 1,45 x J (15) = 21,75 mmCE
F'B' = 1,20 x J = 18 mmCE
- Pertes de charge singulières
BF = 1,45 x Z (12,28) = 17,81 mmCE
F'B' = 1,20 x Z =  14,74 mmCE
- Pertes de charge totales
21,75 + 18 + 17,81 + 14,74 = 72,30 mmCE pour un diamètre de 16x18

On peut remarquer à ce stade des calculs que la 2ème façon à permis de réduire, par rapport à la 1ère façon, les diamètres des tronçons AB B'A' (20x22 contre 26x28), BC C'B' (16x18 contre 20x22) et BF F'B' (16x18 contre 20x22) pour une meilleure efficacité quand à la répartition des pertes de charge. En contre partie, il a fallu augmenter le diamètre des tronçons CD D'C' (16x18 contre 14x16) mais malgré tout, de cette manière le prix de revient de l'installation en a été réduit.

 
puce

Autres circuits (raccordement radiateurs).

puce

Diamètre pour le tronçon DI I'D' (radiateur R4)
- Perte de charge disponible
1000 - 109,11 - 476,80 - 189,84 = 224,25 mmCE
Dans ces tronçons qui sont propre au raccordement du radiateur, on peut facilement voir que le rapport J/Z de 55/45% ne peut être utilisé car les pertes singulières seront plus importantes que les pertes linéiques et ceci en raison de la présence du robinet, du coude ou té de réglage, du radiateur lui même et des brusques changements de vitesse du fluide à l'entrée et à la sortie du radiateur. On va donc prendre un rapport J/Z de 40/60% et procéder comme pour le circuit le plus défavorisé.
- Valeur moyenne de J pour cette perte de charge
J = (224,25 x 0,40) / (0,80 + 0,20) = 89,70 mmCE/m
Débit des tronçons : R4 = 53 l/h
Comme pour les tronçons BF F'B', on sort du cadre du tableau A. En procédant comme pour ces derniers, on trouve un débit immédiatement supérieur de 55 l/h pour un diamètre de 10x12 ce qui donne une valeur pour J de 8 mmCE/m
- Valeur moyenne de J
8 mmCE/m
- Valeur moyenne de Z
Z = 8 x (0,60 / 0,40) = 12 mmCE/m
- Pertes de charge par frottement
(0,80 + 0,20)  x J (8) = 8 mmCE
- Pertes de charge singulières
(0,80 + 0,20)  x Z (12) = 12 mmCE
- Pertes de charge totales
8 + 12 = 20 mmCE au lieu de 224,25 mmCE pour un diamètre de 10x12
Donc pour éviter que ce radiateur (R4) ne s'alimente trop au détriment des autres, il va falloir créer une perte de charge artificielle de 224,25 - 20 = 204,25 mmCE pour un débit de 53 l/h. Perte de charge qui sera créée à l'aide du coude ou té de réglage situé sur la conduite de retour chauffage du radiateur. Pour savoir le nombre de tours nécessaires à la création de cette perte artificielle, se reporter sur l'abaque livrée avec l'organe d'équilibrage. Le réglage en nombre de tours se fait toujours à partir de l'organe d'équilibrage fermé en comptant le nombre de tours d'ouverture.
puce

Diamètre pour les tronçons HC C'H' (radiateur R3)
Procéder le la même façon que pour le tronçon DI I'D'.
- Perte de charge disponible
1000 - 109,11 - 476,80 = 414,09 mmCE
Rapport J / Z de 40% / 60%
- Valeur moyenne de J pour cette perte de charge
J = (414,09 x 0,40) / (0,80 + 0,20) = 165,64 mmCE/m
Débit des tronçons : R3 = 166 l/h
comme pour les précédents tronçons, on sort à nouveau du tableau A. Débit 168 l/h pour un diamètre de 14x16 et une valeur pour J de 11 mmCE/m
- Valeur moyenne de J
11 mmCE/m
- Valeur moyenne de Z
- Valeur de Z
Z = 11 x (0,60 / 0,40) = 16,50 mmCE/m
- Pertes de charge par frottement
(0,80 + 0,20)  x J (11) = 11 mmCE
- Pertes de charge singulières
(0,80 + 0,20)  x Z (16,50) = 16,50 mmCE
- Pertes de charge totales
11 + 16,50 = 27,50 mmCE au lieu de 414,09 mmCE pour un diamètre de 14x16
- Perte de charge artificielle
414,09 - 27,50 = 386,59 mmCE pour un débit de 166 l/h
puce

Diamètre pour les tronçons FJ J'F' (radiateur R1)
- Perte de charge disponible
1000 - 109,11 - 72,30 = 818,59 mmCE
- Valeur moyenne de J pour cette perte de charge
J = (818,59 x 0,40) / (0,80 + 0,20) = 327,44 mmCE/m
Débit des tronçons : R1 = 211 l/h
- Nouvelle valeur moyenne de J
 J = 17 mmCE/m pour un diamètre de 14x16 et un débit de 216 l/h
- Valeur moyenne de Z
Z = 17 x (0,60 / 0,40) = 25,50 mmCE/m
- Pertes de charge par frottement
(0,80 + 0,20)  x J (17) = 17 mmCE
- Pertes de charge singulières
(0,80 + 0,20)  x Z (25,50) = 25,50 mmCE
- Pertes de charge totales
17 + 25,50 = 42,50 mmCE au lieu de 818,59 mmCE pour un diamètre de 14x16
- Perte de charge artificielle
818,59 - 42,50 = 776,09 mmCE pour un débit de 211 l/h
On remarque que plus on se rapproche du circulateur plus la charge disponible est élevée et donc plus grande sera la perte de charge artificielle. R1 est le radiateur le plus favorisé.
puce

Diamètre  pour les tronçons FG G'F' (radiateur R2)
- Perte de charge disponible
1000 - 109,11 - 72,30 = 818,59 mmCE
Dans ce cas ci, le rapport J/Z de 55/45% peut être à nouveau utilisé car les longueurs de conduites de raccordement sont plus importantes que pour les tronçons précédents.
- Valeur moyenne de J pour cette perte de charge
J = (818,59 x 0,55) / (7,5 + 0,80 + 0,20 + 7,5) = 28,14 mmCE/m
Débit des tronçons : R2 = 78 l/h
- Nouvelle valeur moyenne de J
 J = 15 mmCE/m pour un diamètre de 10x12 et un débit de 80 l/h
- Valeur moyenne de Z
Z = 15 x (0,45 / 0,55) = 12,28 mmCE/m
- Pertes de charge par frottement
(7,5 + 0,80 + 0,20 + 7,5)  x J (15) = 240 mmCE
- Pertes de charge singulières
(7,5 + 0,80 + 0,20 + 7,5)  x Z (12,28) = 196,48 mmCE
- Pertes de charge totales
240 + 196,48 = 436,48 mmCE au lieu de 818,59 mmCE pour un diamètre de 10x12
- Perte de charge artificielle
818,59 - 436,48 = 382,11 mmCE pour un débit de 78 l/h
 
puce

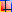Récapitulatif.

puce

Diamètres
tronçons AB B'A' 20x22
tronçons BC C'B' 16x18
tronçons CD D'C' 16x18
tronçons DE E'D' 14x16
tronçons BF F'B' 16x18
tronçons FJ J'F' 14x16 branchement radiateur R1
tronçons FG G'F' 10x12 branchement radiateur R2
tronçons HC C'H' 14x16 branchement radiateur R3
tronçons DI I'D' 10x12 branchement radiateur R4
tronçons DE E'D' 14x16 branchement radiateur R5
 
puce

Pertes de charge totales
La perte de charge de référence s'élève à 899,51 mmCE
 
puce

Pertes de charge artificielles
tronçons FJ J'F' (R1) 776,09 mmCE pour un débit de 211 l/h
tronçons FG G'F' (R2) 382,11 mmCE pour un débit de 78 l/h
tronçons HC C'H' (R3) 386,59 mmCE pour un débit de 166 l/h
tronçons DI I'D' (R4) 204,25 mmCE pour un débit de 53 l/h
tronçons DE E'D' (R5) 100,49 mmCE pour un débit de 106 l/h
Exemple de pertes de charge artificielles (nombre de tours d'ouverture) avec des coudes de réglage sar (Comap).
Pour le radiateur R1 :
débit 211 l/h, perte de charge artificielle 776,09 mmCE
Coude de réglage en 1/2"
nombre de tours d'ouverture = 2 tours 3/4
Pour le radiateur R2 :
débit 78 l/h, perte de charge artificielle 382,11 mmCE
Coude de réglage en 3/8"
nombre de tours d'ouverture = 2 tours 3/4
Pour le radiateur R3 :
débit 166 l/h, perte de charge artificielle 386,59 mmCE
Coude de réglage en 1/2"
nombre de tours d'ouverture = 3 tours
Pour le radiateur R4 :
débit 53 l/h, perte de charge artificielle 204,25 mmCE
Coude de réglage en 3/8"
nombre de tours d'ouverture = 2 tours 1/2
Pour le radiateur R5 :
débit 106 l/h, perte de charge artificielle 100,49 mmCE
Coude de réglage en 1/2"
nombre de tours d'ouverture = 3 tours 1/2

A la réalisation des travaux, dans le cas où les longueurs des conduites sont conformes aux calculs, une perte de charge artificielle sera à ajouter à celle existante pour tenir compte de la HM réelle du circulateur, dans l'exemple 1250 mmCE donc 1250 - 1000 = 250 mmCE de perte de charge artificielle en plus pour chaque radiateur. Le fait de laisser cette HM en l'état va augmenter légèrement le débit de chaque radiateur et par la même augmenter l'écart moyen des températures (température moyenne du radiateur moins température de la pièce) ce qui se traduira par une petite émission supplémentaire des radiateurs qu'il sera alors possible de corriger en réduisant légèrement la température de départ chaudière.

Le croquis ci-dessous montre le nombre de tours d'ouverture pour le radiateur R1 sur un coude de réglage 1/2" sar (Comap).



A partir de là, nous pouvons représenter graphiquement les courbes caractéristiques du circulateur et du circuit. Pour les courbes du circulateur, on reporte celles du constructeur (il est possible de tracer ses courbes à partir d'une fonction mathématique ajustée mais trop complexe pour être expliquée ici) et pour celle du circuit, on définie la résistance hydraulique (R) de la manière suivante :
R = J / D2
J en mCE
D en m3/h
R caractérise les frottements et obstacles s'opposant au déplacement du fluide. Nous pouvons constater que les pertes de charge ne sont pas proportionnelles au débit, puisque entre la vitesse 1 et la vitesse 3, le débit augmente de 54,16% alors que les pertes de charge augmentent de 137,67%.
Pour tracer la courbe, il suffit de multiplier R par les différents débits à la puissance 2. Dans le cadre de l'exemple, R = 0,89951 / 0,6142 = 2,386. Exemple, pour la vitesse 1, le débit étant de 720 l/h, la perte de charge correspondante est :
J = 2,386 x 0,722 = 1,2369 mCE (1237 mmCE)



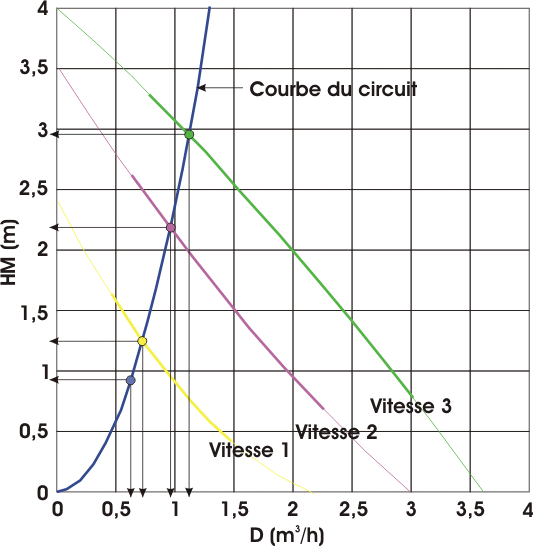
Sur le graphique nous pouvons lire les différentes valeurs, soit :
- Pour les valeurs calculées,  899,51 mmCE pour 614 l/h (point bleu)
- Pour le fonctionnement en vitesse 1, 1237 mmCE pour 720 l/h (point jaune, fonctionnement qui sera adopté dans le cadre de l'exemple)
- Pour le fonctionnement en vitesse 2, 2199 mmCE pour 960 l/h (point mauve)
- Pour le fonctionnement en vitesse 3, 2940 mmCE pour 1110 l/h (point vert)
Note : les traits en gras représentent les plages de fonctionnement optimales pour chaque vitesse.
 
puce

Conduites en Per (rétube).
Pour l'utilisation de conduites en rétube, les calculs se déroulent de la même manière que pour des conduites en cuivre. Il faut dans un 1er temps définir le radiateur le plus défavorisé, donc le plus éloigné du collecteur qui est lui même le plus éloigné de la chaudière. On parle ici de collecteurs car il est difficile de concevoir une autre façon de faire pour réaliser une installation de qualité (l'utilisation de conduites en Per sous gaine permet leur remplacement). C'est une erreur d'utiliser des tés pour le Per et encore plus si les conduites sont dans une chape ou une dalle. Ceci dit, calculer la longueur du circuit le plus défavorisé, du radiateur jusqu'à la chaudière. Définir la perte de charge moyenne de J en fonction de la HM du circulateur, et procéder comme expliqué plus haut. La seule différence est que ce type d'installation concentre les débits de tous les radiateurs au niveau des collecteurs, donc faire attention d'additionner tous les débits de tous les radiateurs raccordés aux collecteurs de l'étage afin de définir le diamètre des colonnes d'alimentation.
Un rapport J/Z de 55/45% ou 50/50% peut être adopté pour ce type de raccordement. Le choix du rapport J/Z doit être fait de manière arbitraire en fonction de la configuration de l'installation.
Utiliser de préférence, comme diamètre minimum, du 13x16 afin d'éviter les risques de bouchage dû aux boues de chauffage, ainsi que du Per avec BAO (barrière anti-oxygène). Ne pas oublier non plus l'adjonction d'un inhibiteur de corrosion afin de limiter au maximum la production de boues de chauffage.

- 2ème exemple :
Pour définir J avec cette méthode, il faut avoir, comme pour le précédent exemple, une plage d'utilisation afin d'avoir une charge suffisante et pour le circulateur et pour éviter des conduites surdimensionnées ainsi qu'une charge maximale pour éviter de trop grandes vitesses qui engendreraient des bruits désagréables. Je pense que la plage de 5 à 20 mmCE/m est acceptable. Plage que j'ai définie de manière arbitraire et empirique. Je ne vais pas ici développer tout le processus de calcul car trop long et compliqué. De toutes manières, il est expliqué en détail à la page "Formules/Tableaux". Les résultats ont été obtenus avec le classeur Excel "Pertes de charge.xls" qui est disponible en téléchargement.
Pour démontrer la méthode, je vais utiliser en partie l'exemple précédent, à savoir les puissances et le croquis. Pour effectuer les calculs, un outils informatique est quasi obligatoire si on veux s'en sortir avec les formules. Comme on est sensé ne pas avoir de tableau (comme le tableau A) pour estimer les valeurs approximatives de J en fonction de la puissance donc du débit, il va falloir y aller à tâtons et procéder par élimination des diamètres qui ne correspondent pas, d'où la nécessité d'un outil informatique ou d'une calculatrice scientifique. Il suffit, une fois le choix fait de la T° de départ du fluide et de la chute (DeltaT), de jouer sur les diamètres pour avoir la valeur de J en fonction de la puissance du tronçon et prendre le diamètre qui donne pour J une valeur se trouvant dans la plage de 1 à 20 mmCE/m.
Donc pour l'exemple, T° de départ = 70°C, DeltaT = 15°C.
J doit être cherché en 1er de façon à avoir la vitesse du fluide qui sera utilisé pour le calcul de Z. Les puissances doivent être majorées de 20% pour tenir compte des émissions thermiques des conduites afin que les radiateurs aient le débit d'équilibre thermique nécessaire.
On va, comme pour l'exemple précédent, commencer par le circuit du radiateur le plus défavorisé.

puce

Circuit le plus défavorisé.
- Pertes de charge linéiques.

puce

Diamètre pour le tronçon DE/E'D'
Puissance de 1500W x 1,2 = 1800W
Diamètre 10x12 : J = 22,71
Diamètre 12x14 : J = 9,58
Diamètre 14x16 : J = 4,62
Le diamètre sera 12x14 pour une vitesse du fluide de 0,26 m/s
puce

Diamètre pour le tronçon CD/D'C'
Puissance de (1500 + 750) x 1,2 = 2700
A partir de maintenant, on dispose d'une base de départ qui est le diamètre du tronçon précédent.
Diamètre 10x12 : J = 46,00
Diamètre 12x14 : J = 19,35
Diamètre 14x16 : J = 9,31
Le diamètre sera 12x14 pour une vitesse du fluide de 0,39 m/s
puce

Diamètre pour le tronçon BC/C'B'
Puissance de (1500 + 750 + 2350) x 1,2 = 5520
Diamètre 14x16 : J = 32,47
Diamètre 16x18 : J = 17,19
Diamètre 20x22 : J = 5,95
Le diamètre sera 16x18 pour une vitesse du fluide de 0,45 m/s
puce

Diamètre pour le tronçon AB/B'A'
Puissance de (1500 + 750 + 2350 + 3000 + 1100) x 1,2 = 10440
Diamètre 16x18 : J = 52,86
Diamètre 20x22 : J = 18,20
Diamètre 26x28 : J = 5,21
Le diamètre sera 20x22 pour une vitesse du fluide de 0,54 m/s
puce

Pertes de charge linéiques totales du circuit
DE/E'D' : 13,6 x 9,58 = 130,29
CD/D'C' : 17,4 x 19,35 = 336,69
BC/C'B' : 13,35 x 17,19 = 229,50
AB/B'A' : 3 x 18,20 = 54,60
Total = 130,29 + 336,69 + 229,50 + 54,60 = 751,08
Donc 751,08 mmCE de pertes de charge linéique.

- Pertes de charge singulières.
Le croquis utilisé pour l'exemple est un schéma de principe assez simple où les singularités ne sont pas représentées. Si il est facile de connaître le nombre de robinets, coudes de réglage, tés, etc... il n'en est pas de même pour les coudes à la cintrette, ceux du commerce et différents casses. On va donc les imaginer pour l'exemple et qui d'ailleurs, serait susceptible d'être dans une installation réelle comme pour un renfoncement de fenêtre qui justifierait 8 coudes 90° à la cintrette ou du commerce.

puce

Singularités du tronçon DE/E'D'
Diamètre 12x14
Vitesse du fluide 0,26 m/s
9 coudes 90° à la cintrette d'un rayon de 4,2cm
R > 3xD : Cs = 0,7
2 coudes 90° MF du commerce R = 1cm
R < 1,5xD : Cs = 1,5
1 té avec flux sortant du té (Départ) : Cs = 0,8
1 té avec flux entrant dans le té (Retour) : Cs = 0,7
1 robinet de radiateur équerre : Cs = 5
1 coude de réglage :Cs = 5
1 radiateur : Cs = 3
9 coudes 90° R 4,2cm : Z = 20,62
2 coudes 90° R 1cm : Z = 9,82
1 té flux sortant : Z = 2,62
1 té flux entrant : Z = 2,29
1 robinet équerre : Z = 16,36
1 coude de réglage : Z = 16,36
1 radiateur : Z = 13,09
Pertes totales : Z = 20,62 + 9,82 + 2,62 + 2,29 + 16,36 + 16,36 + 13,09 = 81,16 mmCE
A ce résultat, on va ajouter 25% pour les éventuelles pénétrations de brasure et la marge pour le petit raccord oublié.
Donc Z = 81,16 x 1,25 = 101,45 mmCE
puce

Singularités du tronçon CD/D'C'
Diamètre 12x14
Vitesse du fluide 0,39 m/s
6 coudes 90° R 5,5cm : Cs = 0,7
1 té flux entrant : Cs = 0,7
1 té flux sortant : Cs = 0,8
6 coudes 90° R 5,5cm : Z = 30,93
1 té flux entrant : Z = 5,15
1 té flux sortant : Z = 5,89
Pertes totales : 30,93 + 5,15 + 5,89 = 41,97 mmCE
Z = 41,97 x 1,25 = 52,47
puce

Singularités du tronçon BC/C'B'
Diamètre 16x18
Vitesse du fluide 0,45 m/s
6 coudes 90° R 7,5cm : Cs = 0,5
4 casses 45° R 7,5cm : Cs = 0,3
1 té flux entrant : Cs = 0,7
1 té flux sortant : Cs = 0,8
6 coudes 90° R 7,5cm : Z = 29,21
4 casses 45° R 7,5cm : Z = 11,69
1 té flux entrant : Z = 6,82
1 té flux sortant : Z = 7,79
Pertes totales : 29,21 + 11,69 + 6,82 + 7,79 = 55,51 mmCE
Z = 55,51 x 1,25 = 69,39
puce

Singularités du tronçon AB/B'A'
Diamètre 20x22
Vitesse du fluide 0,54 m/s
8 coudes 90° du commerce R 3cm : Cs = 1
4 coudes 45° du commerce R 3cm : Cs = 0,7
2 vannes à boules : Cs = 0,5
1 chaudière : Cs = 5
8 coudes 90° R 3cm : Z = 114,14
4 coudes 45° R 3cm : Z = 39,95
2 vannes : Z = 14,27
1 chaudière : Z = 71,34
Pertes totales : 114,14 + 39,95 + 14,27 + 71,34 = 239,70 mmCE
Z = 239,70 x 1,25 = 299,63
Ici, on va à nouveau rajouter un pourcentage pour prendre en compte les différents raccords de la panoplie comme la soupape différentielle, doigts de gants des thermomètres, etc... On va prendre ici une valeur de 30%.
Donc Z = 299,63 x 1.30 = 389,52
Les pertes de charge singulières totales pour le circuit le plus défavorisé s'élèvent à : 81,16 + 41,97 + 55,51 + 239,70 = 418,34 mmCE

Pertes de charge totales du circuit le plus défavorisé (J + Z) s'élèvent à :
751,08 + 418,34 = 1169,42 mmCE.
En prenant la HM nominale de la vitesse 1 du circulateur pour le débit de 614 l/h, 1250 mmCE, la perte de charge résultante est de 1250 - 1169,42 = 80,58 mmCE, dans ce cas, le résultat est bon mais il ne faut pas avoir oublié de raccords ou de coudes et bien suivre le cheminement car cette perte résultante est assez mince et une variation des paramètres utilisés pourrait induire une perte de charge plus importante qui pourrait dépasser celle du circulateur et entraîner une sous alimentation du radiateur le plus défavorisé.
Il suffit maintenant de procéder de la même manière pour calculer le reste du circuit. Dans cet exemple, le rapport J/Z est de 64/36% :
J = 751,08 / 1169,42 x 100 = 64,22%
Z = 418,34 / 1169,42 x 100 = 35,77%

Croquis de l'installation pour l'exemple.

 

Tableau A

Les valeurs ont étés obtenues avec une température de départ du fluide de 55°C et un DeltaT de 10°C.
 

  Diamètres en mm des conduites
Cuivre Rétube
10X12 12X14 14X16 16X18 20X22 26X28 30X32 38X40 10X12 13X16 16X20 20x25
J en mmCE/m 1 16 (0,06) 33 (0,08) 49 (0,09) 59 (0,08) 111 (0,10) 228 (0,12) 338 (0,13) 646 (0,16) 16 (0,06) 46 (0,10) 59 (0,08) 111 (0,10)
2 32 (0,11) 42 (0,10) 62 (0,11) 90 (0,12) 166 (0,15) 342 (0,18) 505 (0,20) 961 (0,24) 32 (0,11) 50 (0,10) 90 (0,12) 166 (0,15)
3 35 (0,12) 51 (0,13) 79 (0,14) 114 (0,16) 210 (0,19) 432 (0,23) 637 (0,25) 1211 (0,30) 35 (0,12) 64 (0,13) 114 (0,16) 210 (0,19)
4 36 (0,13) 61 (0,15) 93 (0,17) 135 (0,19) 249 (0,22) 509 (0,27) 751 (0,30) 1426 (0,35) 36 (0,13) 76 (0,16) 134 (0,19) 248 (0,22)
5 42 (0,15) 69 (0,17) 106 (0,19) 153 (0,21) 283 (0,25) 579 (0,30) 854 (0,34) 1618 (0,40) 42 (0,15) 86 (0,18) 153 (0,21) 282 (0,25)
6 46 (0,16) 77 (0,19) 118 (0,21) 171 (0,24) 314 (0,28) 642 (0,34) 947 (0,37) 1794 (0,44) 46 (0,16) 96 (0,20) 170 (0,23) 314 (0,28)
7 51 (0,18) 84 (0,21) 129 (0,23) 186 (0,26) 343 (0,30) 701 (0,37) 1034 (0,41) 1958 (0,48) 51 (0,18) 105 (0,22) 186 (0,26) 343 (0,30)
8 55 (0,19) 91 (0,22) 140 (0,25) 201 (0,28) 371 (0,33) 757 (0,40) 1115 (0,44) 2111 (0,52) 55 (0,19) 114 (0,24) 201 (0,28) 370 (0,33)
9 59 (0,21) 98 (0,24) 150 (0,27) 216 (0,30) 397 (0,35) 809 (0,42) 1192 (0,47) 2256 (0,55) 59 (0,21) 122 (0,26) 215 (0,30) 396 (0,35)
10 63 (0,22) 104 (0,26) 159 (0,29) 229 (0,32) 421 (0,37) 859 (0,45) 1265 (0,50) 2393 (0,59) 63 (0,22) 129 (0,27) 229 (0,32) 420 (0,37)
11 66 (0,23) 110 (0,27) 168 (0,30) 242 (0,33) 445 (0,39) 907 (0,47) 1335 (0,52) 2525 (0,62) 66 (0,23) 137 (0,29) 242 (0,33) 444 (0,39)
12 70 (0,25) 116 (0,28) 177 (0,32) 255 (0,35) 468 (0,41) 953 (0,50) 1403 (0,55) 2652 (0,65) 70 (0,25) 144 (0,30) 254 (0,35) 466 (0,41)
13 73 (0,26) 121 (0,30) 185 (0,33) 267 (0,37) 490 (0,43) 997 (0,52) 1468 (0,58) 2774 (0,68) 73 (0,26) 151 (0,32) 266 (0,37) 488 (0,43)
14 77 (0,27) 127 (0,31) 193 (0,35) 278 (0,38) 511 (0,45) 1040 (0,54) 1530 (0,60) 2892 (0,71) 76 (0,27) 157 (0,33) 277 (0,38) 509 (0,45)
15 80 (0,28) 132 (0,32) 201 (0,36) 290 (0,40) 531 (0,47) 1081 (0,57) 1591 (0,63) 3006 (0,74) 79 (0,28) 164 (0,34) 289 (0,40) 530 (0,47)
16 83 (0,29) 137 (0,34) 209 (0,38) 300 (0,41) 551 (0,49) 1122 (0,59) 1650 (0,65) 3117 (0,76) 83 (0,29) 170 (0,36) 300 (0,41) 549 (0,49)
17 86 (0,30) 142 (0,35) 216 (0,39) 311 (0,43) 571 (0,50) 1161 (0,61) 1707 (0,67) 3224 (0,79) 85 (0,30) 176 (0,37) 310 (0,43) 569 (0,50)
18 89 (0,31) 146 (0,36) 223 (0,40) 321 (0,44) 589 (0,52) 1199 (0,63) 1763 (0,69) 3329 (0,82) 88 (0,31) 182 (0,38) 320 (0,44) 587 (0,52)
19 91 (0,32) 151 (0,37) 230 (0,42) 332 (0,46) 608 (0,54) 1236 (0,65) 1818 (0,71) 3432 (0,84) 91 (0,32) 188 (0,39) 330 (0,46) 606 (0,54)
20 94 (0,33) 156 (0,38) 237 (0,43) 341 (0,47) 626 (0,55) 1272 (0,67) 1871 (0,74) 3532 (0,87) 94 (0,33) 193 (0,40) 340 (0,47) 624 (0,55)
21 97 (0,34) 160 (0,39) 244 (0,44) 351 (0,48) 643 (0,57) 1308 (0,68) 1923 (0,76) 3629 (0,89) 97 (0,34) 199 (0,42) 350 (0,48) 641 (0,57)
22 100 (0,35) 164 (0,40) 251 (0,45) 361 (0,50) 661 (0,58) 1343 (0,70) 1974 (0,78) 3725 (0,91) 99 (0,35) 204 (0,43) 359 (0,50) 658 (0,58)
23 102 (0,36) 169 (0,42) 257 (0,46) 370 (0,51) 678 (0,60) 1377 (0,72) 2024 (0,80) 3819 (0,94) 102 (0,36) 209 (0,44) 369 (0,51) 675 (0,60)
24 105 (0,37) 173 (0,42) 263 (0,47) 379 (0,52) 694 (0,61) 1410 (0,74) 2073 (0,81) 3911 (0,96) 104 (0,37) 214 (0,45) 378 (0,52) 691 (0,61)
25 107 (0,38) 177 (0,43) 270 (0,49) 388 (0,54) 710 (0,63) 1443 (0,75) 2121 (0,83) 4001 (0,98) 107 (0,38) 220 (0,46) 386 (0,53) 708 (0,63)
26 110 (0,39) 181 (0,44) 276 (0,50) 397 (0,55) 726 (0,64) 1475 (0,77) 2168 (0,85) 4089 (1,00) 109 (0,39) 225 (0,47) 395 (0,55) 724 (0,64)
27 112 (0,40) 185 (0,45) 282 (0,51) 405 (0,56) 742 (0,66) 1507 (0,79) 2215 (0,87) 4176 (1,02) 112 (0,40) 229 (0,48) 404 (0,56) 739 (0,65)
28 115 (0,41) 189 (0,46) 288 (0,52) 414 (0,57) 758 (0,67) 1538 (0,80) 2260 (0,89) 4262 (1,04) 114 (0,40) 234 (0,49) 412 (0,57) 754 (0,67)
29 117 (0,41) 193 (0,47) 294 (0,53) 422 (0,58) 773 (0,68) 1569 (0,82) 2305 (0,91) 4346 (1,06) 117 (0,41) 239 (0,50) 420 (0,58) 770 (0,68)
30 119 (0,42) 197 (0,48) 299 (0,54) 430 (0,59) 788 (0,70) 1599 (0,84) 2349 (0,92) 4429 (1,08) 119 (0,42) 244 (0,51) 429 (0,59) 784 (0,69)
  Débit en litres/heure (vitesse en m/s)

Tableau B
 

  Diamètres en mm des conduites
Acier
12x17 15x21 20x27 26x34 33x42 40x49 50x60
J en mmCE/m 1 33 (0,08) 53 (0,08) 107 (0,09) 221 (0,12) 424 (0,14) 717 (0,16) 1312 (0,19)
2 42 (0,10) 72 (0,11) 160 (0,14) 327 (0,17) 626 (0,20) 1054 (0,23) 1925 (0,27)
3 49 (0,12) 91 (0,14) 201 (0,18) 411 (0,22) 784 (0,25) 1318 (0,29) 2403 (0,34)
4 58 (0,14) 107 (0,17) 236 (0,21) 482 (0,25) 919 (0,30) 1543 (0,34) 2810 (0,40)
5 66 (0,16) 122 (0,19) 267 (0,24) 545 (0,29) 1039 (0,34) 1743 (0,39) 3171 (0,45)
6 73 (0,18) 135 (0,21) 296 (0,26) 603 (0,32) 1148 (0,37) 1924 (0,43) 3499 (0,50)
7 80 (0,20) 147 (0,23) 322 (0,28) 656 (0,34) 1248 (0,41) 2092 (0,46) 3801 (0,54)
8 86 (0,21) 159 (0,25) 347 (0,31) 706 (0,37) 1342 (0,44) 2248 (0,50) 4083 (0,58)
9 92 (0,23) 169 (0,27) 370 (0,33) 753 (0,39) 1430 (0,46) 2395 (0,53) 4349 (0,62)
10 97 (0,24) 180 (0,28) 392 (0,35) 797 (0,42) 1514 (0,49) 2535 (0,56) 4600 (0,65)
11 103 (0,25) 189 (0,30) 414 (0,37) 840 (0,44) 1594 (0,52) 2668 (0,59) 4840 (0,68)
12 108 (0,27) 199 (0,31) 434 (0,38) 880 (0,46) 1670 (0,54) 2795 (0,62) 5070 (0,72)
13 113 (0,28) 208 (0,33) 453 (0,40) 919 (0,48) 1744 (0,57) 2917 (0,64) 5290 (0,75)
14 118 (0,29) 216 (0,34) 472 (0,42) 957 (0,50) 1814 (0,59) 3035 (0,67) 5502 (0,78)
15 122 (0,30) 225 (0,35) 490 (0,43) 993 (0,52) 1883 (0,61) 3149 (0,70) 5707 (0,81)
16 127 (0,31) 233 (0,37) 507 (0,45) 1028 (0,54) 1949 (0,63) 3259 (0,72) 5905 (0,84)
17 131 (0,32) 241 (0,38) 524 (0,46) 1063 (0,56) 2013 (0,65) 3365 (0,74) 6098 (0,86)
18 135 (0,33) 248 (0,39) 541 (0,48) 1096 (0,57) 2076 (0,67) 3469 (0,77) 6285 (0,89)
19 139 (0,34) 256 (0,40) 557 (0,49) 1128 (0,59) 2136 (0,69) 3570 (0,79) 6467 (0,91)
20 143 (0,35) 263 (0,41) 573 (0,51) 1160 (0,61) 2195 (0,71) 3669 (0,81) 6644 (0,94)
21 147 (0,36) 270 (0,42) 588 (0,52) 1190 (0,62) 2253 (0,73) 3765 (0,83) 6817 (0,96)
22 151 (0,37) 277 (0,44) 603 (0,53) 1220 (0,64) 2310 (0,75) 3859 (0,85) 6986 (0,99)
23 155 (0,38) 284 (0,45) 618 (0,55) 1250 (0,65) 2365 (0,77) 3950 (0,87) 7151 (1,01)
24 159 (0,39) 291 (0,46) 632 (0,56) 1278 (0,67) 2419 (0,79) 4040 (0,89) 7313 (1,03)
25 162 (0,40) 297 (0,47) 646 (0,57) 1307 (0,68) 2472 (0,80) 4128 (0,91) 7472 (1,06)
26 166 (0,41) 304 (0,48) 660 (0,58) 1334 (0,70) 2524 (0,82) 4215 (0,93) 7627 (1,08)
27 169 (0,42) 310 (0,49) 673 (0,60) 1361 (0,71) 2575 (0,84) 4299 (0,95) 7780 (1,10)
28 172 (0,42) 316 (0,50) 687 (0,61) 1388 (0,73) 2625 (0,85) 4383 (0,97) 7930 (1,12)
29 176 (0,43) 322 (0,51) 700 (0,62) 1414 (0,74) 2674 (0,87) 4464 (0,99) 8077 (1,14)
30 179 (0,44) 328 (0,52) 712 (0,63) 1440 (0,75) 2723 (0,88) 4545 (1,00) 8222 (1,16)
  Débit en litres/heure (vitesse en m/s)

 

puce Connaître diverses valeurs d'un radiateur.
Les résultats obtenus ici ne seront qu'approximatifs car trop de facteurs rentrent en ligne de compte, comme la précision des appareils de mesure (thermomètres, débitmètre) , les différents DeltaTTm/Ti (voir légende) utilisés par les fabricants pour leurs calculs, 90/70/20 ou 90/75/20 (température du fluide à l'entrée du radiateur / température du fluide à la sortie du radiateur / température de la pièce) donc 60 ou 55°C ceci pour les radiateurs antérieur à 1997 et 75/65/20 donc 50°C pour les radiateurs postérieur à 1997, les différents DeltaTTd/Tr, en général 20 ou 15°C pour les radiateurs antérieur à 1997 et maintenant 10°C alors que la profession utilise toujours, en général, un DeltaTTd/Tr de 15°C pour éviter les débits trop importants et donc les pertes de charge plus élevées. Le fait que l'installateur ou l'ingénieur thermicien est ou non surdimensionné le radiateur pour fonctionner à une température de chaudière plus basse et ceci afin de réduire les coûts d'exploitation (ce qu'il est conseillé de faire). Malgré tout, les résultats suffiront pour avoir une bonne idée de la situation.
Légende :
Td = température de départ (température à l'entrée du radiateur)
Tr = température de retour (température à la sortie du radiateur)
Tm = température moyenne du radiateur Tm = (Td + Tr) / 2
Ti = température de la pièce
Q = puissance en Watts
D = débit en litres/heure
p = masse volumique de l'eau en kg/litre en fonction de sa température (voir tableau à la page "Formules/Tableaux") p doit être pris à la température moyenne du radiateur : (Td + Tr) / 2
c = coefficient de chaleur spécifique de l'eau c = 1,1627
n = exposant de la loi d'émission n = 1,287 (valeur moyenne pour l'extrapolation de puissance à un autre DeltaTTm/Ti )
DeltaTTm-Ti = différence de température entre la température  moyenne du fluide et celle de la pièce. Température de la pièce qui doit être prise au centre de celle-ci et à la hauteur de 1,5 m du sol. DeltaTTm-Ti = ((Td + Tr) / 2) - Ti
DeltaTTd-Tr = différence de température du fluide entre l'entrée et la sortie du radiateur DeltaTTd-Tr = Td - Tr
DeltaTTm-Ti_connu = DeltaT (température moyenne du fluide - température de la pièce) connu, sert de base pour connaître la puissance du radiateur à un DeltaTTm/Ti différent (calcul par extrapolation)
DeltaTTm-Ti_désiré = DeltaT (T° moyenne du fluide - T° de la pièce) désiré, sert de but pour connaître la puissance du radiateur à un DeltaTTm/Ti voulu (calcul par extrapolation)
 
puce Connaître le débit d'eau du radiateur.
Il est assez difficile de connaître le débit d'eau dans un radiateur par calcul car il faut partir de la puissance annoncée par le fabricant, seulement elle dépend du DeltaTTd-Tr choisi par celui-ci pour la définir, 10, 15 ou 20°C ainsi que du DeltaTTm-Ti 60, 55 ou 50°C. Pour un résultat assez fiable, l'emploi d'un débitmètre est conseillé, sinon, par calcul, voici comment procéder :
Pour avoir le DeltaTTd-Tr, utiliser 2 thermomètres, 1 à l'entrée et 1 à la sortie du radiateur. Ils peuvent être à applique afin d'éviter tout démontage et bricolage de raccordement, seulement la précision ne sera pas vraiment idéale. Un thermomètre électronique peu aussi être utilisé mais attention à l'émissivité qui peu influencer légèrement la température indiquée.
Comme le fabricant annonce la puissance de son radiateur pour un DeltaTTm-Ti donné (60, 55 ou 50°C) et qu'il est peu probable que celui au moment des prises de mesures soit identique, il va donc falloir trouver la puissance approximative en fonction du DeltaTTm-Ti au moment des mesures. Dans un 1er temps, prendre les températures entrée/sortie du radiateur, trouver le DeltaTTm-Ti comme indiqué dans la légende, ensuite, trouver la puissance du radiateur à ce DeltaTTm-Ti par extrapolation en utilisant la formule suivante :
Q = QFabricant x ((DeltaTTm-Ti_désiré  /  DeltaTTm-Ti_connu)n)
Exemple :
QFabricant = 1700 W
T° de la pièce = 20°C
T° entrée = 66°C
T° sortie = 58°C
DeltaTTm-Ti_désiré = celui au moment des mesures : ((66 + 58) / 2) - 20 = 42°C
DeltaTTm-Ti_connu = celui annoncé par le fabricant : 50°C
puissance extrapolée :
Q = 1700 x ((42 / 50)1,287) = 1358,30 W
débit :
D = Q / (DeltaTTd-Tr x c x p)
D = 1358,30 / (8 x 1,1627 x 0,9822) = 148,66 l/h
 
puce Connaître le DeltaT entrée/sortie du radiateur.
Il faut pour ceci, connaître la puissance du radiateur ainsi que son débit. Dans un 1er temps, extrapoler la puissance en fonction du DeltaTTm/Ti actuel et ensuite utiliser la formule suivante :
DeltaTTd-Tr = Q / D / c / p
Exemple avec les valeurs de l'exemple précédent :
Q = 1700 x ((42 / 50)1,287) = 1358,30 W
DeltaTTd-Tr = 1358,30 / 148,66 / 1,1627 / 0,9822 = 8 °C
 
puce Connaître la puissance en Watts d'un radiateur.
Pour connaître la puissance en Watts d'un radiateur, 3 valeurs sont nécessaires :
- Le débit en litres/heure
- La température d'entrée du fluide dans le radiateur (Td)
- La température de sortie du fluide dans le radiateur (Tr)
Pour obtenir ces valeurs, il est possible de "bricoler" un raccordement avec 2 flexibles, 2 thermomètres et un débitmètre ainsi que divers raccords. Dans un 1er temps, démonter le radiateur et le poser sur 2 cales en bois d'une hauteur à peu près identique à l'espace qu'il y a entre le bas du radiateur et le sol quand il est accroché au mur puis le raccorder à nouveau à ses conduites d'alimentation en faisant attention à la purge de l'air. Le fait d'utiliser les flexibles, les divers raccords et le débitmètre augmente un peu les pertes de charge et donc réduit le débit, pour compenser, il suffit de rajouter une dizaine de Watts au résultat. Comme précisé plus haut, Il faut savoir que le résultat sera approximatif car le débitmètre et les thermomètres ont une marge d'erreur. Pour cette raison, éviter de prendre des pièces sous dimensionnées afin le limiter les pertes de charge.
La formule est la suivante :
Q = D x DeltaTTd-Tr x c x p
Exemple :
D = 125 l/h
T° Entrée = 60°C
T° Sortie = 53°C
Q = 125 x 7 x 1,1627 x 0,9852 = 1002,39 W
Pour connaître la puissance éventuelle du radiateur annoncée par le fabricant (puissance qui a peut être défini le choix du radiateur par l'installateur ou l'ingénieur thermicien), il faut extrapoler à partir du DeltaTTm-Ti au moment des mesures et savoir si le radiateur est assez récent pour avoir un DeltaTTm-Ti fabricant de 50 °C avec des valeurs prisent de 75/65/20 ce qui donne un DeltaTTd-Tr de 10 °C, ou si il est plutôt ancien et alors avoir un DeltaTTm-Ti de 60 ou 55 °C avec des valeurs prisent de 90/70/20 ou 90/75/20 ce qui donne un DeltaTTd-Tr de 20 ou 15 °C.
Exemple en reprenant les valeurs de l'exemple précédent :
Température  de la pièce = 20°C
Température  moyenne du fluide = 56,5°C
Q = 1002,39 Watts
DeltaTTm-Ti_désiré = celui probable du fabricant avec un radiateur assez récent : 50 °C
DeltaTTm-Ti_connu = celui au moment des mesures : (60 + 53) / 2  - 20 = 36,5 °C
Qfabricant = Q x ((DeltaTTm-Ti_désiré / DeltaTTm-Ti_connu)n)
Qfabricant = 1002,39 x ((50 / 36,5)1,287) = 1502,93
p = 0,9777 pour une T° moyenne du fluide de 70 °C : (75 + 65) / 2
DeltaTTd-Tr à cette puissance = 1503 / 125 / 1,1627 / 0,9777 = 10,57 °C
Dans ce cas ci, le débit de la pompe est correct et la puissance trouvée assez précise car le DeltaTTd-Tr du fabricant est probablement de 10 °C. Si le DeltaTTd-Tr avait été plus grand, il est probable que le débit dans le radiateur est été insuffisant. Si le DeltaTTm-Ti au moment des mesures est différent de celui du fabricant (sûrement inférieur) et que le DeltaTTd-Tr ai une valeur supérieure ou égale à celui utilisé par le fabricant, il est probable que le débit soit insuffisant ou le radiateur sous dimensionné car le DeltaTTd-Tr est proportionnel au DeltaTTm-Ti.
Exemple :
D = 125 l/h
Température d'entrée = 60 °C
Température de sortie = 50 °C
Q = 125 x 10 x 1,1627 x 0,9857 = 1432,71 W
DeltaTTm-Ti_désiré = celui probable du fabricant avec un radiateur assez récent : 50 °C
DeltaTTm-Ti_connu = celui au moment des mesures : (60 + 50) / 2  - 20 = 35 °C
Qfabricant = Q x ((DeltaTTm-Ti_désiré / DeltaTTm-Ti_connu)n)
Qfabricant = 1432,71 x ((50 / 35)1,287) = 2267,34 W
p = 0,9777 pour une température moyenne du fluide de 70 °C
DeltaTTd-Tr à cette puissance = 2267,34 / 125 / 1,1627 / 0,9777 = 15,95 °C
Donc 16 °C au lieu de 10 °C. Ce qui fait que la puissance trouvée est faussée car le débit pour celle-ci avec le DeltaTTd-Tr du fabricant (10°C) devrai être de : 2267,34 / (10 x 1,1627 x 0,9777) = 199 l/h. Comme le DeltaTTd-Tr au moment des mesures est déjà de 10 °C il est fort probable que le débit soit insuffisant ou que le radiateur soit sous dimensionné car il atteint déjà la puissance maxi du fabricant, mais comme précisé plus haut, il y a trop de facteurs entrant en jeu pour pouvoir être catégorique sur ce point. Si par exemple, l'installateur ou l'ingénieur thermicien a utilisé un DeltaTTd-Tr de 15°C le résultat est là, par contre, assez bon. C'est pour cela qu'il est toujours difficile de savoir la puissance réellement installée au moment de l'exécution des travaux si on n'est pas en possession d'un minimum de renseignements.