Pertes de charge J et Z.

Tout fluide circulant dans une conduite perd de sa pression initiale (de sa charge) à chaque mètre parcouru et à chaque passage d'une singularité. Cette perte de charge est due au frottement contre les parois de la conduite (qui est assez faible quand le flux est laminaire ou peu turbulent) et à la forme des singularités qui créent des turbulences. La perte de charge totale en mmCE du circuit le plus défavorisé doit être définie (perte de charge la plus importante) car le circulateur doit pouvoir la vaincre et ceci en maintenant le débit nécessaire à l'installation afin de permettre la circulation du fluide. On appelle cette perte de charge la perte de charge de base ou la perte de charge de référence. Elle sera à prendre en compte pour le choix du circulateur. La perte de charge linéique (J) doit être calculé pour chaque diamètre rencontré en partant du radiateur le plus défavorisé ou de la boucle du plancher chauffant la plus défavorisée ou de tout autre appareil à alimenter en fonction du débit et multiplié par la longueur du dit tuyau et en allant vers la chaudière (ce n'est pas une obligation mais une facilité) et ceci sur la conduite départ et retour du circuit. Une fois les pertes de charge définies pour les différentes conduites, il faudra les additionnées entre elles ainsi que les pertes de charge singulières (Z) afin d'obtenir la perte de charge de base. L'équilibre du circuit se fera à l'aide des coudes et tés de réglages ou tout autre organe d'équilibrage en créant une perte de charge artificielle qui, additionnée aux pertes de charge propre au radiateur ou circuit du plancher chauffant concerné, sera égale à la perte de charge de base ce qui créera un équilibre entre tous les circuits. Attention, dans ce cas là, pour un calcul au plus juste, il faudra calculer les pertes de charge de chaque circuit et les déduire à la perte de charge de base afin de connaître la perte de charge artificielle à créer. En général, il est bon de ne pas dépasser une vitesse de 0,80 à 0,85 m/s et ceci afin d'éviter les risques de bruits et les sifflements au niveau des robinets thermostatiques. Certaines installations fonctionnent avec des vitesses de 1 m/s sans problème, mais une vitesse de 0,75 m/s maximum est une limite de prudence.
La valeur d'une perte de charge est fonction de plusieurs paramètres qui sont étroitement liés entrer eux mais pour plus d'explications voir la page "Les pertes de charge".
 

Calcul des débits (D).

On obtient le débit en litres/h avec la formule suivante :
D = P / (DeltaT x Ce x p x 10^-3) x 1,20  pour les radiateurs.
D en kg/h mais pour plus de facilité on utilise le résultat en litres/h sans avoir un trop grand pourcentage d'erreur.
P = puissance en Watts
DeltaT = chute de température entre le départ et le retour, souvent prise égale à 15°C mais ceci n'est pas une obligation et les radiateurs peuvent même avoir un DeltaT différent les uns des autres. Le DeltaT normalisé est maintenant de 10°C mais la profession utilise encore un DeltaT de 15°C pour le calcul des radiateurs. Seulement, dans ce cas, la puissance normalisée doit être redéfinie, pour cela voir la page "Les radiateurs", paragraphe "Dimensionnement des radiateurs".
Ce= chaleur spécifique de l'eau (1,1628)
p = masse volumique du fluide en kg/m³ pour une température donnée. (pour l'eau, voir tableau)
1,20 étant une valeur de 20% pour les émissions thermiques des conduites de raccordement qui doivent être prisent en compte pour le calcul des débits. La valeur de ces émissions thermiques est fonction de plusieurs paramètres comme le DeltaT entre la température des conduites et celle de l'air ambiant, si elles sont isolées ou non, du diamètre de celles-ci. Le calcul étant assez complexe (voir plus bas), il est courrant de prendre comme valeur 20% qui seront rajoutés à la puissance de chaque radiateur.
D = (Qg + Qr + Qvb) / (DeltaT x Ce x p x 10^-3) pour les planchers chauffants.
Qg = puissance de la grille chauffante en Watts.
Qr =  émissions thermiques en Watts des conduites de raccordement. Ces émissions thermiques ne peuvent pas être interprétées en valeur d'émission surfacique, seulement, ces émissions doivent être prisent en compte pour le calcul du débit du panneau afin d'avoir le débit d'équilibre thermique. De ce fait on va appliquer une formule pour considérer ses émissions en émissions thermiques linéaires. Qr = longueur x (Tm² x Ct).
Tm = température moyenne du fluide.
Ct = 0,0072 pour du 13x16 et 0,0075 pour du 16x20
Qvb = émissions thermiques de la grille chauffante vers le bas qui sont fonction de l'épaisseur de l'isolant.
DeltaT = chute de Température entre le départ et le retour généralement prise égale à 8°C pour un plancher chauffant à charges normales et élevées et 3°C pour un plancher chauffant à charges limites mais ces températures ne sont pas une obligation car parfois pour éviter un appoint thermique il est possible de réduire la chute afin d'augmenter l'écart moyen des températures dont dépendantes directement les émissions surfaciques de la grille chauffante.
 

Connaître les déperditions thermiques des conduites.

Les conduites départ/retour chauffage ont des émissions thermiques non négligeables dont il faut tenir compte dans le calcul des débits pour la connaissance des pertes de charge d'un tronçon. Pour cette raison, il est de coutume de prendre 20% de la puissance du radiateur comme émissions thermiques afin de tenir compte de ce fait. Il est possible de ne prendre que 10% si les conduites sont isolées sur une grande partie de leurs longueur.
Toutes fois, il est possible de connaître avec plus d'exactitude les émissions thermiques des conduites. Seulement, dans le cas où ces émissions doivent être prisent en compte pour le calcul des débits (la vitesse du fluide va influencer les pertes de charge) et ceci afin de définir les diamètres des conduites, on en vient au serpent qui se mord la queue car pour connaître les émissions thermiques des conduites, leurs diamètres est nécessaire mais pour connaître leurs diamètres, le débit total est utile et bien évidement, les émissions thermiques sont nécessaires au calcul du débit total. Il est donc plus facile de prendre une valeur de 20% de la puissance du radiateur comme émissions thermiques. Il est malgré tout possible de choisir une valeur arbitraire entre 5 et 25% en fonction de la longueur des conduite et du DeltaT entre température des conduites et température du local.
Dans le cas où malgré tout le débit précis dû aux émissions thermiques réelles est nécessaire, on déterminera les diamètres et les émissions thermiques de proche en proche. C'est à dire, en commençant par prendre une valeur de 20% pour ces émissions afin de définir un diamètre adapté au débit puis de calculer les émissions thermiques pour ce diamètre et de rectifier en fonction du résultat. Dans l'exemple où les émissions thermiques seraient trop différentes des 20% de la puissance du radiateur, le débit serait à recalculer en fonction des émissions réelles et le cas échéant, de redéfinir le diamètre en fonction du débit trouvé. Si le diamètre est modifié, les émissions thermiques seront à recalculer en fonction du nouveau diamètre et ainsi de suite.
Pour connaître les émissions thermiques des conduites, différentes formules sont à utiliser selon le cas où les conduites sont isolées ou non.
 

	Calcul des coefficients thermiques de transmission interne et externe hi et he.   Coefficient hi. hi est le coefficient interne de transmission thermique. Ce coefficient s'obtient avec les formules approchées suivantes et ceci en fonction du régime du fluide, turbulent ou laminaire, et de la nature du fluide (ici l'eau et l'air). - Pour de l'eau dans une conduite en régime turbulent : hi = 2040 x (1 + 0,015 x Tm) x (v0,87 / di0,13) en W/(m².K) - Pour de l'eau dans une conduite en régime laminaire : hi = 1998 x (1 + 0,015 x Tm) x (v0,87 / di0,13) en W/(m².K) - Pour de l'air dans une conduite en régime turbulent : hi = (4,13 + 0,23 x (Tm / 100) - 0,0077 x (Tm / 100)2) x (v0,75 / di0,25) en W/(m².K) - Pour de l'air dans une conduite en régime laminaire : hi = (4,13 + 0,16 x (Tm / 100) - 0,0077 x (Tm / 100)2) x (v0,75 / di0,25) en W/(m².K)   Coefficient he. he est le coefficient externe de transmission thermique. Ce coefficient s'obtient avec les formules approchées suivantes et ceci en fonction du milieu. - Pour une conduite dans l'air, où l'air est en convection libre (ex : conduite dans un local) : he = 5 x ((T1 - T2) / (T2 x de))0,25 en W/(m².K) - Pour une conduite dans l'eau où l'eau est en convection libre (ex : serpentin d'un ballon sanitaire) : he = (18,6 + 20,7 x ((T1 + T2) / 2 )0,5 x ((T1 - T2) / de)0,25 en W/(m².K) Tm = température moyenne du fluide dans la conduite en °C v = vitesse du fluide en m/s di = diamètre intérieur de la conduite en m de = diamètre extérieur de la conduite en m T1 et T2 = températures absolues en K, T1 et T2 = 273,15 + T (pour 20°C, T1 ou T2 = 273,15 + 20 = 293,15 K) Note : pour vérifier si le régime est turbulent ou laminaire, utiliser la formule approchante suivante : Dm = D / di Dm en litres/h par mètre de diamètre de conduite (l/h.m). D étant le débit en litres/h et di le diamètre intérieur du tube en mètre. Le rapport doit être supérieur ou égal à 3300 l/h.m (pour Re = 2321, le nombre est de 3292 l/h.m).
	Calcul du flux de chaleur transmis à travers une paroi courbe. Le flux de chaleur transmis par un fluide à un autre par l'intermédiaire d'une conduite (air ou eau) peut être calculé soit par mètre linéaire [en W/(m.K)] symbolisé par le coefficient linéique Y (repris de la RT2000), soit par mètre carré [en W/(m².K)] et symbolisé par le coefficient surfacique U (lui aussi, repris de la RT2000). Le coefficient surfacique U est représenté par deux coefficients surfaciques, Ui pour le coefficient de transmissions surfacique interne et Ue pour le coefficient de transmissions surfacique externe. 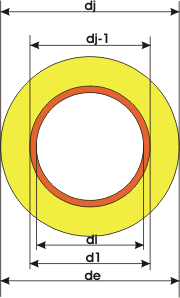Les coefficients de transmission thermique sont obtenus avec les formules suivantes et donnent forcément le même résultat : - Flux thermique linéique global rapporté à la longueur de conduite en W/(m.K) : Y = Pi / (1 / hi x 1 / di + SOMME(1 / (2 x Ldaj)) x ln(dj / dj-1) + 1 / he x 1 / de) - Flux thermique surfacique interne global rapporté à la surface interne de la conduite en W/(m².K) : Ui = 1 / (1 / hi + SOMME(di / (2 x Ldaj)) x ln(dj / dj-1) + 1 / he x di / de) - Flux thermique surfacique externe global rapporté à la surface externe de la conduite en W/(m².K) : Ue = 1 / (1 / hi x de / di + SOMME(di / (2 x Ldaj)) x ln(dj / dj-1) + 1 / he) Pi = 3,1415 di et de = respectivement diamètre intérieur et extérieur de la conduite en m Lda = coefficient Lambda de conductivité thermique du métal ou du matériau en W/(m.K). 380 W/(m.K) pour le cuivre. ln = logarithme népérien
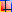	Exemples. Prenons un exemple numérique afin de bien appréhender les méthodes de calcul. Soit une conduite en cuivre de 30x32 mm véhiculant une eau à une température moyenne de 70°C avec un débit de 1350 l/h, cette conduite traverse un local sur une longueur de 12 m dont la température ambiante moyenne est de 10°C. Calculer le flux de chaleur transmis de l'eau chaude à l'air du local pour la conduite non isolée et pour la conduite isolée avec coquille de laine de verre de 3 cm d'épaisseur ayant un coefficient Lambda (Lda) de 0,04 W/(m.K). Cas de la conduite non isolée. - Calcul des coefficients hi et he : 1350 nous donne une vitesse de : v = (1350 / 1000 / 3600) / ((0,03 / 2)2 x 3,1415) = 0,53053 m/s Contrôle du régime du fluide dans la conduite : 1350 / 0,03 = 45000 l/h.m, 45000 étant supérieur à 3300, le régime est turbulent. hi = 2040 x (1 + 0,015 x 70) x (0,530530,87 / 0,030,13) = 3800,63 W/(m².K) Ce qui nous donne une résistance thermique superficielle interne (Rsi) de 1 / 3800,63 = 0,000263 m².K/W valeur très faible qui pourrait alors être négligée. Le cuivre ayant un coefficient de conductivité thermique très élevé (380 W/(m.K)), la température superficielle du tube est prise égale à celle du fluide, soit 70°C (elle serait plutôt voisine de 69,85°C). he = 5 x (((273,15 + 70) - (273,15 + 10)) / ((273,15 + 10) x 0,032))0,25 = 8,02 W/(m².K) - Calcul du coefficient de transmission thermique linéique Y : Y = 3,1415 / (1 / 3800,63 x 1 / 0,03 + 1 / (2 x 380) x ln(0,032 / 0,03) + 1 / 8,02 x 1 / 0,032) = 0,8044 W/(m.K) Déperditions thermiques de la conduite : Dep = 0,8044 x (70 - 10) x 12 = 579,17 W - Calcul du coefficient de transmission thermique surfacique interne Ui : Ui = 1 / (1 / 3800,63 + 0,03 / (2 x 380) x ln(0,032 / 0,03) + 1 / 8,02 x 0,03 / 0,032) = 8,5353 W/(m².K) Déperditions thermiques de la conduite : Dep = 8,5353 x 3,1415 x 0,03 x 12 x (70 - 10) = 579,17 W - Calcul du coefficient de transmission thermique surfacique externe Ue : Ue = 1 / (1 / 3800,63 x 0,032 / 0,03 + 0,03 / (2 x 380) x ln(0,032 / 0,03) + 1 / 8,02) = 8,0018 W/(m².K) Déperditions thermiques de la conduite : Dep = 8,0018 x 3,1415 x 0,032 x 12 x (70 - 10) = 579,17 W   Cas de la conduite isolée. Le coefficient hi ne change pas, il reste égal à 3800,63 W/(m².K). Comme la conduite est isolée, la température superficielle de l'isolant sera bien inférieure à celle de la conduite non isolée. Il est assez difficile de connaître de façon exacte la valeur de cette température superficielle mais il est possible de l'approcher en utilisant les différentes résistances thermiques. Comme le coefficient he se trouve dans l'équation pour l'obtention du flux thermique et que de ce dernier dépend la température superficielle extérieure utilisée dans le calcul du coefficient he, il faut procéder par touches successives, ce qui demande l'emploi d'un programme informatique afin de simplifier les calculs. Donc, les résultats présentés ci-dessous ont été préalablement calculés sur tableur Excel. Calcul de la température superficielle externe : Résistance superficielle interne : Rsi = 1 / 3800,63 x 0,092 / 0,03 = 0,0008 m².K/W Résistance du tube : RTube = 0,092 / (2 x 380) x ln(0,032 / 0,03) = 0,0000078 m².K/W Résistance de l'isolant : RIsolant = 0,092 / (2 x 0,04) x ln(0,092 / 0,032) = 1,2144 m².K/W Température superficielle externe : 70 - (0,6814 x (70 - 10) x (0,0008 + 0,0000078 + 1,2144)) = 20,31°C Coefficient he : he = 5 x (((273,15 + 20,31) - (273,15 + 10)) / ((273,15 + 10) x 0,092))0,25 = 3,965 W/(m².K) Vérification : Résistance superficielle externe : Rse = 1 / 3,965 = 0,2522 m².K/W Résistance thermique totale : Rt = 0,0008 + 0,0000078 + 1,2144 + 0,2522 = 1,4674 m².K/W 70 - (0,6814 x (70 - 10) x 1,4674) = 10°C (les 10°C du local). - Calcul du coefficient de transmission thermique linéique Y : Y = 3,1415 / (1 / 3800,63 x 1 / 0,03 + 1 / (2 x 380) x ln(0,032 / 0,03) + 1 / (2 x 0,04) x ln(0,092 / 0,032) + 1 / 3,965 x 1 / 0,092) = 0,197 W/(m.K) Déperditions thermiques de la conduite : Dep = 0,197 x (70 - 10) x 12 = 141,8 W - Calcul du coefficient de transmission thermique surfacique interne Ui : Ui = 1 / (1 / 3800,63 + 0,03 / (2 x 380) x ln(0,032 / 0,03) + 0,03 / (2 x 0,04) x ln(0,092 / 0,032) + 1 / 3,965 x 0,03 / 0,092) = 2,0897 W/(m².K) Déperditions thermiques de la conduite : Dep = 2,0897 x 3,1415 x 0,03 x 12 x (70 - 10) = 141,8 W - Calcul du coefficient de transmission thermique surfacique externe Ue : Ue = 1 / (1 / 3800,63 x 0,092 / 0,03 + 0,092 / (2 x 380) x ln(0,032 / 0,03) + 0,092 / (2 x 0,04) x ln(0,092 / 0,032) + 1 / 3,965) = 0,6814 W/(m².K) Déperditions thermiques de la conduite : Dep = 0,6814 x 3,1415 x 0,092 x 12 x (70 - 10) = 141,8 W Ceci démontre l'efficacité de l'isolant sur la réduction des pertes thermiques de la conduite. La différence sur les 12 m étant de : 579,17 - 141,8 = 437,37 W Le pourcentage de pertes thermiques supplémentaires dues à l'absence d'isolant est donc de : 579,17 / 141,8 x 100 = 408,44% soit 4 fois plus. Si la conduite n'est pas isolée, la température du fluide au bout des 12 m sera de : T = 70 - ((0,8044 x (70 - 10) x 12) / (1350 / 3600 x 4185,5)) = 69,63°C soit une chute de température de : DeltaT = 70 - 69,63 = 0,37°C Pour un résultat plus précis : T = 70 + (70 - 10) x (1 - EXP((0,8044 x 12) / (1350 / 3600 x 4185,5))) = 69,629°C Dans le cas où la conduite est isolée, la température au bout des 12 m sera de : T = 70 + (70 - 10) x (1 - EXP((0,197 x 12) / (1350 / 3600 x 4185,5))) = 69,91°C soit une chute de température de : DeltaT = 70 - 69,91 = 0,09°C 4185,5 est la capacité thermique massique de l'eau en J/kg.K EXP est la fonction inverse de Ln (ex ou e^ sur les calculatrices) Autre exemple : Soit un tronçon (partie d'un circuit) raccordant un radiateur d'une puissance de 1500 Watts (radiateur R5 de l'exemple à la page "Les radiateurs" voir croquis). Conduite de départ d'une longueur de 7,10 m et d'un diamètre de 14x16 mm, conduite de retour d'une longueur de 6,50 m de même diamètre. Température moyenne du fluide de 60°C pour le départ et de 45°C pour le retour. Température d'ambiance au niveau des conduites, 18°C. Le débit de fluide étant de 106 l/h. Vitesse du fluide : v = (0,106 / 3600) / (0,0072 x 3,1415) = 0,19128 m/s - Conduite de départ : hi = 2040 x (1 + 0,015 x 60) x (0,191280,87 / 0,0140,13) = 1601,18 W/(m².K) he = 5 x (((273,15 + 60) - (273,15 + 18)) / ((273,15 + 18) x 0,016))0,25 = 8,664 W/(m².K) Y = 3,1415 / (1 / 1601,18 x 1 / 0,014 + 1 / (2 x 380) x ln(0,016 / 0,014) + 1 / 8,664 x 1 / 0,016) = 0,4328 W/(m.K) Dep = 0,4328 x (60 - 18) x 7,10 = 129,06 W - Conduite de retour : hi = 2040 x (1 + 0,015 x 45) x (0,191280,87 / 0,0140,13) = 1411,567 W/(m².K) he = 5 x (((273,15 + 45) - (273,15 + 18)) / ((273,15 + 18) x 0,016))0,25 = 7,758 W/(m².K) Y = 3,1415 / (1 / 1411,567 x 1 / 0,014 + 1 / (2 x 380) x ln(0,016 / 0,014) + 1 / 7,758 x 1 / 0,016) = 0,3875 W/(m.K) Dep = 0,3875 x (45 - 18) x 6,50 = 68 W Les déperditions thermiques totales des conduites s'élèvent à : Dep = 129,06 + 68 = 197,06 W Les émissions thermiques des conduites par rapport à la puissance du radiateur sont alors de : 197,06 / 1500 = 0,131 soit un peu plus de 13%. Ici, on voit que la valeur par défaut de 20% est supérieure aux déperditions réelles des conduites mais il est bien évident que si les longueurs ou les températures moyennes étaient différentes le résultat le serait aussi. Il suffirait que les conduites soit plus longues de seulement 3,5 m ou les températures du fluide plus élevées de 10°C pour arriver aux 20%. Le fait de prendre une valeur de 20% par défaut simplifie grandement les calculs et a suffisamment d'exactitude sur la globalité de l'installation pour la prise en compte des pertes thermiques dans les débits sachant que, comme le démontre l'exemple sur la page "Les radiateurs", une carence en débit a plus d'influence sur la température ambiante qu'un excès de débit.
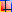	Conclusions. Souvent on ne prend pas en compte les pertes thermiques des conduites alimentant les émetteurs et dans le cas où ces conduites ne sont pas isolées et de grande longueur, la température du fluide ayant servie aux calculs de dimensionnement des émetteurs (généralement la température départ chaudière) est faussée par la chute du fluide dans les dites conduites. La puissance thermique à l'émetteur sera donc plus faible et on sera obligé, soit d'augmenter dans de fortes proportions le débit de fluide avec les inconvénients que ceci risque d'entraîner au niveau des pertes de charge, soit d'augmenter la température du fluide au départ chaudière et ceci au risque de se trouver et limité, dans le cas des conditions extérieures de base, par l'aquastat de chaudière (75°C maxi pour les chaudières actuelles) et en déséquilibre thermique pour les émetteurs les plus proche de la chaudière ayant des pertes thermiques de conduites de raccordement plus faibles. Conclusion, comme dit plus haut, une valeur de majoration de 20% du débit permet de prendre en compte cet état de fait sans grande incidence dans le cas d'un surdimensionnement du débit nécessaire car il suffira de freiner ce débit supplémentaire à l'aide de l'organe d'équilibrage de l'émetteur, et si le débit est laissé en l'état, ceci aura moins d'influence sur la température d'ambiance qu'un manque de débit.

Connaître les déperditions thermiques d'un ballon.

pour connaître les déperditions thermiques d'un ballon de stockage (ballon ECS, ballon tampon, etc...), il est possible d'utiliser les formules ci dessous (Règlementation thermique, règles Th-C). Elles prennent aussi en compte un pourcentage de perte dû aux ponts thermiques des conduites piquées sur le ballon ainsi que les probables petites imperfections de l'isolation.
Dep = H_B x DeltaT
Dep = déperditions thermiques totales en W
DeltaT = différence de température entre la température moyenne de stockage et celle de l'ambiance
H_B = déperditions thermiques en W/K
H_B = A x U x (1 + (0,05 / V))
A = surface extérieur du ballon en m²
A= r² x Pi x 2 + d x Pi x h
r = rayon extérieur du ballon en m
Pi = 3,1415
d = diamètre extérieur du ballon en m
h = hauteur extérieure du ballon en m
V = volume extérieur du ballon en m³
V = r² x Pi x h
U = coefficient de transmission surfacique en W/(m².K)
U = 1 / (0,13 + R)
R = résistance thermique de l'isolation en m².K/W
R = e / Lda
e = épaisseur de l'isolation en m
Lda = coefficient lambda de conductivité thermique de l'isolant en W/(m.K) qui peut être pris égal à 0,04 W/(m.K), coefficient moyen.
Un exemple pour illustrer :
d = 0,60
h = 1,5
e = 0,08
DeltaT = 60 - 20 = 40 (60°C de température de stockage, 20°C de température du local)
V = 0,3² x 3,1415 x 1,5 = 0,424 m³
A = 0,3² x 3,1415 x 2 + 0,6 x 3,1415 x 1,5 = 3,39 m²
R = 0,08 / 0,04 = 2 m².K/W
U = 1 / (0,13 + 2) = 0,469 W/(m².K)
H_B = 3,39 x 0,469 x (1 +(0,05 / 0,424)) = 1,777 W/K
Dep = 1,777 x 40 = 71,08 W
Le ballon a une déperdition thermique de 71,08 W.
 

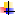Connaître au bout de combien de temps une conduite va geler et éclater.

Admettons une conduite en cuivre de 30x32 isolée avec des coquilles de laine de verre épaisseur 30 mm et un coefficient lambda de 0,04 W/m/K. Dans cette conduite circule de l'eau à une température de 70 °C. La conduite passe dans un coffre situé à l'extérieur où règne une température de -5°C quand la température extérieure est elle de -10°C. Dans l'hypothèse où le circulateur tombe en panne, au bout de combien de temps la conduite va t'elle éclater, sachant qu'une conduite éclate quand à peu près un quart de son volume d'eau c'est transformé en glace ? Ceci bien évidemment, en considérant que la température extérieure reste constante durant tout le processus, ce qui est faux vu la durée de celui-ci, mais cela peut donner une idée.
Solution :
Le calcul est fait pour un mètre de conduite.
A l'instant où le circulateur tombe en panne, 1 m de conduite contient une énergie (calculée à partir de 0 °C) de :
Q = V x C x T_eau
V est le volume en litre de la conduite, V = r² x 3,1415 x 1000
C est la chaleur massique de l'eau en kJ/kg (capacité qu'a un matériau à absorber ou restituer la chaleur). pour l'eau, 4,1855 kJ/kg.K
T_eau est la température de l'eau dans la conduite
Exemple numérique :
V = 0,015² x 3,1415 x 1000 = 0,70
Q = 0,70 x 4,1855 x 70 = 205,09 kJ (Comme 1 Wh = 3,6 kJ, la quantité d'énergie en W est de : 205,09 / 3,6 = 56,969 W.)
Les déperditions de la conduite s'élèvent à :
he = 5,5 + 3,1 / 0,032^0,25 = 12,83
Y = 3,1415 / (1 / (2 x 0,04) x ln(0,092 / 0,032) + 1 / (12,83 x 0,032)) = 0,2
Les déperditions linéiques sont égales à 0,2 W/m/K. Comme 1 W = 1 J.s (1 joule par seconde) 0,2 W = 0,0002 kJ.s
Les déperditions de la conduite sont fonction du DeltaT (différence entre la température de l'eau et celle du coffre), elles sont donc d'autant plus grande que le DeltaT est important. A chaque seconde, l'énergie cédée à l'extérieur s'élève à : 0,0002 x DeltaT. Pour la première seconde, l'énergie perdue est égale à : Dep = 0,0002 x (70 - -5) = 0,015 kJ. Comme l'énergie contenue dans la conduite vient de se réduire (205,09 - 0,015 = 205,075 kJ), la température de l'eau dans celle-ci c'est aussi réduite, ce qui influe sur le DeltaT et bien évidemment sur les déperditions. Donc, pour la seconde suivante, le DeltaT doit être recalculé. La quantité d'énergie pour 1 °C d'écart ne variant pas (V x C = 0,70 x 4,1855 = 2,92985 kJ), la première seconde écoulée, la température de l'eau dans la conduite vient de passer de 70 °C à : 205,075 / 2,92985 = 69,995 °C. Le nouveau DeltaT est maintenant de : 69,995 - -5 = 74,995 °C.
Comme il est impossible d'effectuer les calculs manuellement pour chaque seconde (c'est le laps de temps qui donne le meilleur résultat), un outils informatique est nécessaire. Le classeur Excel  Itération.xls en fichier zip contient une page permettant de connaître, et la durée pour atteindre 0 °C et la durée pour atteindre l'éclatement de la conduite.
Pour l'exemple, on va déterminer une durée où le DeltaT sera constant pour ensuite chuter au bout de ce laps de temps (ceci a pour effet de raccourcir la durée réelle mais de cette façon, on saisi mieux le processus). Nous allons prendre une durée arbitraire de 3 heures.
3 h = 10800 secondes.
Dep = 0,0002 x (70 - -5) x 10800 = 162 kJ. (45 W)
Au bout de ce 1er laps de temps, l'énergie restante est maintenant de :
205,09 - 162 = 43,09 kJ
la température de l'eau est maintenant de :
43,09 / 2,92985 = 14,70 °C
le DeltaT est à présent de :
14,70 - -5 = 19,70 °C.
Prenons un second laps de temps de 3 h.
Dep = 0,0002 x 19,70 x 10800 = 42,55 kJ. (11,82 W)
énergie restante :
43,09 - 42,55 = 0,54
la température de l'eau :
0,54 / 2,92985 = 0,18 °C
le DeltaT :
0,18 - -5 = 5,18 °C.
A ce stade, il ne faut plus que quelques secondes pour que l'eau dans la conduites atteigne 0°C :
0,54 / (0,0002 x 5,18) = 521 (8 minutes et 41 secondes)
Il a fallut 6 heures 8 minutes et 41 secondes pour que l'eau soit à 0°C dans la conduite.
Le classeur Excel donne une durée de 11 heures 04 minutes et 36 secondes. On voit bien qu'en prenant un laps de temps supérieur à la seconde, on raccourci la durée et ceci est dû au fait qu'on utilise un DeltaT constant alors qu'il change à chaque seconde. Plus le DeltaT est faible, plus les déperditions le sont aussi d'où une plus grande durée.
A ce stade, l'eau est à 0°C mais encore à l'état liquide.
La congélation s'effectue à température constante (0°C) et pour que l'eau passe de l'état liquide à l'état solide, il faut lui soutirer une quantité d'énergie de 333,6 kJ/kg (79,70 kCal/kg) disons 334 kJ/kg. Pour arriver à l'éclatement (environ un quart de la contenance et ceci dépend encore de la malléabilité du cuivre(recuit ou non)), les déperditions devront donc être de :
(0,70 / 4) x 334 = 58,45 kJ
Comme le processus s'effectue à température constante, les déperditions sont elles aussi constantes et égales à :
0,0002 x Abs(-5) = 0,001 kJ
La durée de congélation afin d'atteindre l'éclatement sera de :
58,45 / 0,001 = 58450 secondes
Ce qui donne en heures, minutes et secondes :
58450 / 3600 = 16,2361 donc 16 heures
(58450 - (3600 x 16)) / 60 = 14,16 donc 14 minutes
850 - (60 x 14) = 10 secondes
16 heures 39 minutes et 10 secondes
Dans notre exemple, la durée totale jusqu'à l'éclatement, à partir de l'arrêt du circulateur est de :
6:08:41 + 16:39:10 = 22:47:51 Le classeur Excel donne 27:22:40.
Partant de ce principe, il est tout à fait possible de connaître le temps mis par un ballon contenant de l'eau chaude pour atteindre la température du local où il se trouve, mais le problème est que le temps mis est important et ceci à cause du faible DeltaT en fin de durée. Le temps est d'autant plus important que la contenance du ballon est grande puisque l'énergie disponible pour 1 °C est fonction du volume ( V x C).
 

Connaître le débit de combustible.

Pour connaître le débit de combustible en m³ de gaz ou en litres de fuel, il est nécessaire de connaître le débit total de l'eau de chauffage circulant dans la chaudière en m³/h ainsi que le DeltaT entre la T° de l'eau de départ chauffage et celle du retour chaudière. Il faut aussi connaître le rendement de l'installation. Ensuite la formule est :
Debit_Comb. = (Ve x 1,1628 x DeltaT) / (PCI x n)
Ve = débit du fluide caloporteur
PCI = pouvoir calorifique inférieur du combustible en KWh par litre ou m³ :
Gaz de ville PCI = 10,53
Gaz propane PCI = 25,70
Fuel PCI = 10,25
n = rendement de l'installation
Pour un logement individuel, on ne prend en compte que les pertes par les fumées car on ne peut pas estimer dans quelle mesure les déperditions de la chaudière contribuent au chauffage du logement. Les pertes par les fumées sont fonction de la T° des fumées, de la T° de l'air comburant (T° de l'air au niveau du brûleur) ainsi que du taux de CO₂. Un exemple :
T° des fumées = 180°C
T° de l'air = 20°C
Taux de CO₂ = 13%
A l'aide d'un abaque, les pertes par les fumées sont de 7,2% donc le rendement de combustion est de 92,8%
Donc, pour le calcul du débit de combustible par heure :
Débit = 1,2 m³
DeltaT = 15°C
Pour du fuel :
Debit_Comb. = (1,2 x 1,1627 x 15) / (10,25 x 0,928) = 2,2 l/h
Pour du gaz de ville :
Debit_Comb. = (1,2 x 1,1627 x 15) / (10,53 x 0,928) = 2,142 m³/h
Pour du gaz propane :
Debit_Comb. = (1,2 x 1,1627 x 15) / (25,70 x 0,928) = 0,877 m³/h
Comme il n'est pas possible de connaître le taux de CO₂ sans un appareil approprié il est possible de prendre un taux de rendement moyen de 0,90 pour avoir une idée approximative du débit.
 

Connaître le taux de rendement de la chaudière.

Pour connaître le taux de rendement de la chaudière, il y a 2 façons.
- 1 : Comme expliqué plus haut, il faut connaître le taux de CO₂ ainsi que les T° des fumées et celle de l'air comburant puis utiliser un abaque.
- 2 : La formule a utiliser est l'inverse de celle pour savoir le débit de combustible :
n = (VE x 1,1627 x DeltaT) / (Debit_Comb. x PCI)
Ici il faut connaître le débit de combustible. Pour le gaz de ville, il suffit de prendre un chronomètre, de mettre la chaudière en marche forcée et de voir le volume consommé dans un laps de temps au compteur puis de le calculer pour une heure. Pour le fuel c'est un peu plus compliqué car il faut connaître la pression de la pompe, le calibre du gicleur et avoir aussi une règle de calcul.
Avec l'exemple précédant pour le fuel :
n = (1,2 x 1,1627 x 15) / (2,2 x 10,25) = 0,928 donc 92,8%.
 

Connaître les besoins annuel en chauffage.

Afin d'avoir une estimation approximative de consommation de combustible, ce qui peut être intéressant pour définir le volume de stockage du fuel ou du gaz propane, il est nécessaire de connaître les besoins annuels en chauffage. Pour ceci, plusieurs paramètres sont utiles :
- 1) Le coefficient de déperditions thermiques H, en kW/K (voir la page "Calcul des déperditions" dans la partie Déperditions)

- 2) Les DJU (degrés jour unifiés) en base x. La base couramment utilisée est la base 18 c'est à dire 18 °C de température intérieure corrigée donc, sans prise en compte des apports gratuits qui est aussi la température extérieure de non chauffage (Tnc). Il est possible de calculer les DJU pour une autre température. Les DJU sont calculés de la manière suivante : 18 - (moyenne journalière des températures mini/maxi). Toutes ces températures sont ensuite ajoutées pour avoir les valeurs par mois.
Une légère différence existe entre la température moyenne journalière pour un enregistrement horaire et la température moyenne mini/maxi. Une petit exemple :
Températures relevées heure par heure le 12 janvier 2010 :

La température moyenne pour ce 12 janvier 2010 est de -9,5375 °C, la température moyenne Mini/Maxi est de -9,3 °C soit une différence de 2,5%.

Ces valeurs mensuelles vont être ajoutées sur environ 7 mois, période moyenne de chauffage allant du 15 octobre au 15 mai (durée qui dépend aussi des régions). Il est possible d'obtenir ces valeurs auprès de Météo France moyennant finances. Ci-dessous un tableau avec les valeurs pour quelques villes. Pour les calculs, utiliser les valeurs de la ville la plus proche. Si la température mensuelle est connue et bien sûr obtenue par mesure horaire, il est possible de connaître les DJU du mois considéré, exemple Mulhouse température mensuelle pour janvier 0,8 °C, DJU = (18 - 0,8) x 31 = 533 °C.

- 3) L'intermittence ou facteur d'intermittence. Sur une période suffisamment longue, l'énergie thermique nécessaire au chauffage d'un local donné est, en première approximation, proportionnelle à l'aire comprise entre la courbe représentant l'évolution de la température intérieure, en fonction du temps, et celle représentant l'évolution de la température extérieure.
Lorsque le maintien du niveau thermique de confort devient inutile, essentiellement en période d'inoccupation (nuit, fin de semaine, période de congés), tout abaissement de la température intérieure se traduit par une diminution de l'énergie consommée par l'installation de chauffage.
Plus l'abaissement de la température est prononcé, plus cet abaissement est maintenu longtemps à l'intérieur de la période d'inoccupation et plus les économies d'énergie qui en résultent sont grandes.
La valeur du facteur d'intermittence est fonction de plusieurs paramètres, comme l'inertie du bâtiment, les plages d'abaissement de la régulation, la température choisie pour les plages d'abaissement, etc...Le coefficient souvent utilisé par défaut est de 0,85. Si les plages de marche réduite et normale sont identiques pour toute la semaine, il est possible de calculer les DJU de façon un peu plus précise. Exemple, admettons que la période de marche soit de 16 heures à une température de non chauffage de 17 °C pour la période confort et de 8 heures à 14 °C pour la période réduite (en températures corrigées des apports internes), les DJU prenant en compte ces deux périodes seront de :
Dans un premier temps, calculer la température moyenne mensuelle avec la formule suivante :
T_Mensuelle = 18 - DJU₁₈ / NB_Jours
NB_Jours étant le nombre de jours dans le mois
T_Mensuelle = 18 - 533 / 31 = 0,8 °C
Température moyenne intérieure sur la journée :
Ti_M = (17 x 16 + 14 x 8) / 24 = 16 °C
DJU = (16 - 0,8) x 31 = 471,2 °C
Dans le cadre de cet exemple, le coefficient d'intermittence à partir des DJU du mois de janvier est donc de :
471,2 / 533 = 0,88
Ce calcul est à effectuer pour chaque mois et ces coefficients seront ensuite moyenner.
Comme indiqué plus haut, l'inertie du logement joue un rôle important dans la valeur du coefficient d'intermittence, si l'inertie est grande, la relance nécessitera plus d'énergie pénalisant ainsi l'application de l'intermittence. Il en est de même pour la température en période de marche réduite, plus elle est basse, plus la durée de relance augmente.

- 4) Les pertes fatales (pertes quasi inévitables). Comme pour l'intermittence, il est assez difficile d'estimer ces pertes. Une partie d'entre elles, sont les pertes par les fumées et leur pourcentage est fonction du rendement de la chaudière. Les autres pertes sont assez diverses comme les déperditions de la chaudière qui sont fonction de son isolation. Il est difficile d'estimer ces pertes car on ne connaît pas dans quelle mesure est contribuent au chauffage du logement. Par exemple, si la chaudière se trouve dans la cuisine, ses déperditions participent au chauffage du logement par contre si elle est à la cave et que celle-ci est non isolée, une partie de ses déperditions est cédée à l'extérieur et une partie contribue au chauffage du logement en réduisant légèrement le DeltaT entre la pièce où se trouve la chaudière et celle du dessus. Il en est de même pour les conduites alimentant les émetteurs. On va donc estimer un pourcentage de pertes fatales d'environ 20% donc un coefficient de 0,80.

- 5) En dernier lieu, si le logement est très bien situé, la prise en compte des apports thermiques externes (solaires). Il est assez difficile de définir le coefficient qui permet de prendre en compte ces apports car ces derniers sont fonction de bien trop de paramètres. Il est possible de prendre en première approximation une valeur pour A de 0,9.

Maintenant que toutes ces valeurs sont obtenues, il suffit d'utiliser le procédé de calcul ci-dessous :
Besoins_Ch = (24 x DJU x H x I x A) / Ptes
24 = 24 heures (coefficient de transformation des degrés jour en degrés heure)
DJU = Degrés jour unifiés
H = Coefficient de déperditions du logement en kW/K
A des fins de simplifications, H peut être obtenu de la manière suivante :
H = V x U_bât  / 1000
V = Volume du logement en m³
U_bât = Coefficient d'isolation
V = volume en m³ du logement ou de la pièce
U_bât est le coefficient (ici détourné puisque normalement en W/(m².K) ) des déperditions en W/(m³/K).
U_bât = 0,75 W/(m³.K) habitation conforme à la RT 2000 (construit après le 2 juin 2001 mais bon nombre de logements antérieurs à cette date étaient déjà conformes à la RT 2000).
U_bât = 0,90 W/(m³.K) habitation très bien isolée.
U_bât = 1 W/(m³.K) habitation bien isolée.
U_bât = 1,2 W/(m³.K) habitation mal isolée.
U_bât = 1,4 W/(m³.K) habitation non isolée.
1000 = Pour avoir le résultat en KW
I = Intermittence
Ptes = Pertes fatales
Voici un exemple :
Une maison de 120 m² avec une hauteur sous plafond de 2,5 m située dans la région Lyonnaise.
Maison conforme à la RT 2000 donc U_bât = 0,75
Facteur d'Intermittence, I = 0,85
Coefficient de pertes Fatales, Ptes = 0,80
Coefficient de prise en compte des apports thermiques, A = 0,9
Coefficient de déperditions thermiques H :
H = 120 x 2,5 x 0,75 = 225 W/K soit 0,225 kW/K
DJU pour Lyon :
octobre 192 / 2 = 96
novembre = 347
décembre = 460
janvier = 471
février = 369
mars = 327
avril = 234
mai = 124 / 2 = 62
DJU = 96 + 347 + 460 + 471 + 369 + 327 + 234 + 62 = 2366
Besoins_Ch = (24 x 2366 x 0,225 x 0,85 x 0,9) / 0,80 = 12217
Les besoins en chauffage s'élèvent à 12217 KWh/an
Besoins en combustible :
Besoins_Comb. = Besoins_Ch / (PCI x n)
Valeurs PCI, voir plus haut
n est le rendement de combustion du générateur avec une valeur par défaut de 0,9 pour une chaudière standard et 1,03 pour une chaudière à condensation.
Pour le fuel en litres :
Besoins_Comb = 12217 / (10,25 x 0,9) = 1324,3 litres
Pour le gaz de ville en m³ :
Besoins_Comb = 12217 / (10,53 x 0,9) = 1289,1 m³ (1126,4 m³ pour une chaudière à condensation)
Pour le gaz propane en m³ :
Besoins_Comb = 12217 / (25,70 x 0,9) = 528,19 m³
Si la chaudière fournie l'ECS, il faut totaliser les besoins en chauffage sur 7 mois plus les besoins en ECS sur 11 mois (1 mois peu être déduit pour les vacances).
 

Connaître les besoins en ECS.

Pour pouvoir estimer les besoins annuels en ECS, il faut connaître la consommation journalière par personne. Ces valeurs sont obtenues de manière empirique et elles varient de 30 à 60 litres. Un volume de 50 litres par jour et par personne peut être utilisé pour obtenir des résultats suffisamment exacts. La T° de stockage doit aussi être définie. La valeur généralement utilisée se situe entre 50 et 60°C. Il faut aussi connaître la température moyenne annuelle de l'eau froide. Cette valeur se situe en général aux alentours de 10°C. Comme pour les besoins en chauffage, les pertes fatales sont aussi à prendre en considération. Ces pertes comprennent les déperditions du ballon d'ECS, qui sont fonction de la qualité de son isolation, du DeltaT entre la température de stockage et celle de l'air ambiant. Ces pertes sont aussi dus aux déperditions des conduites d'ECS, du refroidissement de l'eau à l'intérieur de celles-ci après un soutirage, eau qui a été chauffée et qui sera envoyée à l'égout au prochain soutirage. Il est difficile d'estimer avec exactitude le pourcentage de pertes fatales donc, pour cette raison, on va prendre une valeur de 25% ce qui donne un coefficient de 0,75. Ces valeurs une fois obtenues, la formule à utiliser est la suivante :
Besoins_ECS = (Vp x Nbp x 30,41 x 11 x 1,1627 x DeltaT) / (1000 x Ptes)
Vp = Volume en litre par personne et par jour
Nbp = Nombre de personnes occupant le logement
30,41 = Nombre de jours par mois sur une moyenne annuelle (365 / 12)
11 = 11 Mois car un mois est pris en compte pour les vacances
1,1627 = Chaleur spécifique de l'eau
1000 = Pour résultats en KW
Ptes = Pertes fatales
Voici un exemple :
4 personnes occupent le logement, l'ECS est stockée à 55°C et la T° de l'eau froide est de 10°C.
Besoins_ECS = (50 x 4 x 30,41 x 11 x 1,1627 x 45) / (1000 x 0,75) = 4668
Donc 4668 KW seront nécessaires à la production d'ECS ce qui donne une consommation annuelle de combustible de :
Pour le fuel en litres :
Besoins_Comb = 4668 / (10,25 x 0,9) = 506 litres
Pour le gaz de ville en m³ :
Besoins_Comb = 4668 / 10,53 = 492,5 m³
Pour le gaz propane en m³ :
Besoins_Comb = 4668 / 25,70 = 201,8 m³
Avec l'exemple pour les besoins annuels de chauffage si on veux savoir la capacité de stockage du fuel il faut savoir la consommation totale donc 11187 + 4668 = 15855 ce qui donne une consommation de 15855 / (10,25 x 0,9) = 1718,7 litres. Dans ce cas, il faudra prévoir une capacité de 2000L afin de n'avoir qu'un remplissage annuel.

DJU pour quelques villes.

Définir le diamètre et la section d'un conduit de fumées.

Pour assurer une marche normale et sans problème d'une chaudière, le conduit de fumées doit être de dimension suffisante, avoir le moins de pertes de charge possible. Il doit être le plus étanche possible car c'est sa dépression qui assure en grande partie l'évacuation des gaz brûlés et elle doit être en mesure de vaincre les pertes de charge. Une formule relative peut être utilisée pour définir le diamètre minimum en fonction de la hauteur du conduit de fumées et de la puissance en Watts de la chaudière ; D = 0,02 x (P / h^0,5).
D = diamètre en mm
P = puissance en Watts de la chaudière
h = hauteur en mètres du conduit de fumées
Exemple :
Une chaudière de 24 KW
Une hauteur de conduit de 8 mètres
D = 0,02 x (24000 / 8^0,5) = 169,7
Conduit normalisé supérieur = 180mm
Surface du conduit en cm² = ((3,14 x 169,7²) / 4) / 100 = 226,07
Pour avoir la dimension en cm correspondante en section carrée = 226,07^0,5 = 15,04.
Il est évident que selon la puissance de la chaudière et la hauteur du conduit de fumées le diamètre et la section obtenus sera relativement faible.
Exemple :
Une chaudière de 17 KW
Une hauteur de conduit de 11 mètres
D = 0,02 x (17000 / 11^0,5) = 102,5
Dans ce cas, il faudra choisir le diamètre normalisé supérieur donc 125mm.
Pour ce qui est de la section carrée :
Surface du conduit en cm² = ((3,14 x 102,5²) / 4) / 100 = 82,48
Section carrée = 82,48^0,5 = 9,08
Le boisseau normalisé et couramment employé est 15 x 15.
Attention ! le diamètre ou la section du conduit de fumées ne devra en aucun cas être inférieur à celui de la buse de sortie de la chaudière.
Diamètre normalisés en mm : 125, 139, 153, 167, 180, 200.
Je n'indique pas les diamètres inférieurs car je les déconseille fortement pour une utilisation en conduit de fumées comme par exemple pour un tubage.