 |
Pertes de charge.
Les coefficients qui représentent les pertes de charge d'une conduite
sont au nombre de deux, les pertes de charge linéiques qui représentent
l'usure tout au long de la conduite (dans les parties droites) symbolisées
par la lettre J, qui est une constante et les pertes de charge singulières qui représentent
les pertes de charge dues à la résistance locale occasionnée par les
différents raccords et appareils, représenté
par la lettre Z.
 |
Pertes de charge linéiques
(J).
La formule générale pour calculer la perte de charge linéique d'une conduite est
:
- en mètre de colonne de fluide par mètre de conduite (mCF/m)
J = Cpe / Di x v2 / (2 x g)
- en Pascals par mètre de conduite (Pa/m)
J = Cpe / Di x p x v2 / 2
- en millibar par mètre de conduite (mbar/m)
J = Cpe / Di x p x v2 / 2 x 0,01
où :
p est la masse volumique du fluide en kg/m3 pour une
température donnée.
g est l'accélération de la pesanteur, environ 9,81 m/s2
Pour convertir en mètre de colonne d'eau (mCE) les pertes de charge qui sont
en mètre de colonne de fluide (mCF), il y a lieu de prendre en compte la
masse des fluides considérés. Par convention, la masse volumique de l'eau
est prise à une température de 4 °C, soit 1000 Kg/m3.
La perte de charge en mètre de colonne d'eau devient :
J = Cpe / Di x v2 / (2 x g) x (pf / peau),
en mCE/m
Le fluide considéré (pf) peut être de l'eau à une température
différente de 4 °C.
Pour convertir les pertes de charge en Pa, multiplier les pertes de charge
en mCF par la masse volumique du fluide et l'accélération de la pesanteur :
JPa = JmCF x p x g
Note : pour le mètre de colonne d'eau (mCE), p = 1000 Kg/m3 car
c'est la masse volumique de référence (JPa = JmCE x
1000 x g). Pour avoir J en millimètre de colonne d'eau, diviser directement
par g (JmmCE = JPa / g).
et l'inverse :
JmCF = JPa / p / g
Pour la vitesse moyenne du fluide dans la conduite :
v = D / 3600 / S
ou D est le débit et S la section de la conduite, dans les unités
correspondantes.
Pour la section :
S = (Di2 x Pi) / 4 ou r2 x Pi
Exemple :
Une conduite en cuivre de 12 mm de diamètre intérieur (12 x 14 mm)
E = 0,0000015 m
Le radiateur à alimenter a une puissance de 1750 W
La température moyenne de l'eau est de 60 °C
Le DeltaT voulu est de 15 °C
Débit :
D = 1750 / (15 x 1,163 x 0,98325) = 102,02 l/h
Section de la conduite :
S = 0,0062 x 3,14 = 0,000113 m²
Vitesse du fluide :
v = 0,10202 / 3600 / 0,000113 = 0,25 m/s
Viscosité cinématique :
vc = -2,2183992 x 10-12 x 603 + 0,00051252585
x 10-6 x 602 - 0,043254681 x 10-6 x 60 +
1,6993718 x 10-6 = 0,0000004751 m²/s
Viscosité dynamique (juste pour information) :
vd = 0,0000004751 x 983,25 = 0,0004671 Pa.s (467,14 uPa.s)
Nombre de Reynolds :
Re = 0,25 x 0,012 / 0,0000004751 = 6314
Re limite :
ReLimite = 3158 + 48000 x 0,0000015 / 0,012 = 3164
Le régime est bien turbulent puisque supérieure à 3164.
coefficient de perte de charge :
A = -2 x Log10((0,0000015 / 0,012) / 3,71 + 12 / 6314) = 5,4269
B = -2 x Log10((0,0000015 / 0,012) / 3,71 + 2,51 x A / 6314) =
5,3186
C = -2 x Log10((0,0000015 / 0,012) / 3,71 + 2,51 x B / 6314) =
5,3359
Cpe = (5,4269 - ((5,4269 - 5,3186)2) / (5,4269 + 5,3359 - (2
x 5,3186)))-2 = 0,03515
J = 0,03515 / 0,012 x 0,252 / (2 x 9,81) x (983,25 / 1000) =
0,009175 mCE/m (9,175 mmCE/m)
en Pa :
à partir de JmCE
J = 0,009175 x 1000 x 9,81 = 90 Pa/m
J = 0,03515 / 0,012 x 983,25 x 0,252 / 2 = 90 Pa/m
en mbar :
J = 0,03515 / 0,012 x 983,25 / 2 x 0,252 x 0,01 = 0,9 mbar/m
La conduite est considérée comme hydrauliquement lisse :
6314 x 0,035150,5 x (0,0000015 / 0,012) = 0,148 bien inférieur à
200.
J sera multiplié par la longueur du tronçon en mètre (calculer J pour
chaque diamètre et débit) pour obtenir les pertes de charge linéiques totales
du tronçon et ajouter les pertes de charge de chaque tronçon pour avoir les
pertes de charge linéiques totales du circuit.
|
 |
Pertes de charge
singulières (Z).
On appelle perte de charge singulière la perte de charge due à
la résistance locale occasionnée par un raccord (té, coude,
vanne, raccord de jonction divers, etc...) ou par un appareil (chaudière, radiateur,
échangeur, etc...). Toute déformation de la veine de fluide, de
changement de direction et de changement de section engendre une perte de
charge singulière.
Ici, 2 méthodes sont expliquées pour calculer les pertes de charge
singulières, la méthode directe où chaque singularité est caractérisée par
un coefficient (noté
 , Cs sera utilisé ici
pour la suite) et la méthode par estimation du rapport J/Z. , Cs sera utilisé ici
pour la suite) et la méthode par estimation du rapport J/Z.
Il est assez facile de calculer les pertes de charge linéiques mais beaucoup
plus complexe de calculer les pertes de charge singulières. Par exemple,
dans un coude la circulation du fluide engendre des force centrifuges qui
augmentent la pression sur la paroi externe de la courbe et la diminue sur
la paroi interne créant ainsi une diminution de la vitesse sur l'extérieur
de la courbe et de par la conservation de l'énergie, une augmentation de la
vitesse dans l'intérieur de la courbe créant un tourbillon juste après le
changement de direction. Il faudra attendre une longueur d'approximativement
10 diamètres pour que le flux retrouve son régime. Si à la sortie de ce
coude se trouve un autre coude, la multiplication par 2 du coefficient de singularité d'un coude
pris isolément n'est plus juste car la présence du second coude, selon son
orientation, va augmenter de 2,5 ou
même 3 fois la valeur de l'ensemble et l'ajout d'un coefficient à l'autre va induire une sous estimation de la perte de charge de ces
deux singularités.
La formule générale pour calculer Z est la suivante :
- en mètre de colonne de fluide (mCF)
Z = Cs x v2 / (2 x g)
- en Pascals (Pa)
Z = Cs x p x v2 / 2
- en millibar (mbar)
Z = Cs x p x v2 / 2 x 0,01
 |
Méthode directe.
Il est très difficile de connaître avec suffisamment de précision les différents
coefficients qui caractérisent les pertes de charge singulières. Ci-dessous
sont données quelques formules pour obtenir les coefficients de certains
singularités et des valeurs tabulées dans le tableau :
Augmentation brusque :
Cs = (1 - S2 / S1)2
Réduction brusque :
Cs = 0,5 x (1 - S1 / S2)
Augmentation progressive :
Cs = 0,62 x (1 - (S2 / S1)2)2
Réduction progressive :
Cs = 0,05
Té avec séparation des courants
 :
:
Cs = 0,5 + 1 / (VLat / VCom)2
Té avec réunion des courants
 :
:
Cs = 3 - 3 / (VLat / VCom) + 2 / (VLat / VCom)2
Té avec réunion des courants, branche rectiligne
 (2) :
(2) :
Cs = 0,55 / (VRec / VCom)2 + 0,45 / (VRec
/ VCom) - 1
Té avec réunion des courants, branche latérale
 (1)
:
(1)
:
Cs = (1 - 0,66 x (DiLat / DiCom)2 + 0,26 x (DiLat
/ DiCom)2)2 x (1 + 2 x (DiLat /
DiCom)2 / (VLat / VCom) - 1 / (VLat
/ VCom)2)
Té avec séparation des courants, branche rectiligne
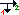 (2) :
(2) :
Cs = 0,4 x (1 / (VRec / VCom) - 1)2
Té avec séparation des courants, branche latérale
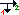 (1)
:
(1)
:
Cs = 1 + 1 / (VLat / VCom)2
Où :
S1 grande section et S2 petite section
VRec, VLat et VCom sont les vitesses
respectives
DiLat et DiCom sont les diamètres respectifs
Filtre à tamis cylindrique maille 0,6 mm
Diamètre 3/8" : Cs = 13,2
Diamètre 1/2" : Cs = 7,2
Diamètre 3/4" : Cs = 5,8
Diamètre 1" : Cs = 4,9
Diamètre 1/1/4" : Cs = 4,7
Diamètre 1/1/2" : Cs = 4,6
Filtre à tamis cylindrique maille 0,25 mm
Diamètre 3/8" : Cs = 14,7
Diamètre 1/2" : Cs = 9,2
Diamètre 3/4" : Cs = 7,4
Diamètre 1" : Cs = 7,3
Diamètre 1/1/4" : Cs = 6,2
Diamètre 1/1/2" : Cs = 6,5
Robinets de radiateur à ouverture maximale (Oventrop série standard A et RF)
Diamètre 3/8" : Cs = 21
Diamètre 1/2" : Cs = 55
Diamètre 3/4" : Cs = 184
Coudes ou tés de réglage à ouverture maximale (Oventrop série Combi 4, 3 et
2)
Diamètre 3/8" : Cs = 13
Diamètre 1/2" : Cs = 35 (dans l'exemple plus bas, le Cs du coude de
réglage Comap grand ouvert est de 21,91)
Diamètre 3/4" : Cs = 116
Vanne d'équilibrage à ouverture maximale (Oventrop série Hydrocontrol R)
Diamètre 3/8" : Cs = 4,7 (Di = 12,5 mm)
Diamètre 1/2" : Cs = 7 (Di = 16 mm)
Diamètre 3/4" : Cs = 11 (Di = 21,6 mm)
Diamètre 1" : Cs = 11 (Di = 27,2 mm)
Diamètre 1/1/4" : Cs = 7 (Di = 35,9 mm)
Diamètre 1/1/2" : Cs = 6,4 (Di = 41,8 mm)
Vanne 3 voies (Oventrop Tri M)
Diamètre 3/4" : Cs = 17
Diamètre 1" : Cs = 21
Diamètre 1/1/2" : Cs = 52
Chaudières
P <= 60 kW : Cs = 1,8
P > 60 < 100 kW : Cs = 3,4
Coefficient Cs pour les radiateurs en raccordement diamètre 3/8" :
L < 1 m Cs = 1,78
L >= 1 m Cs = 2,3
Coefficient Cs pour les radiateurs en raccordement diamètre 1/2" :
L < 1 m Cs = 2,88
L >= 1 m Cs = 3,71
Coefficient Cs pour les radiateurs en raccordement diamètre 3/4" :
L < 1 m Cs = 0,76
L >= 1 m Cs = 1,03
Les coefficients Cs des radiateurs indiqués ci-dessus ont été obtenus en
partant d'un abaque constructeur indiquant les pertes de charge. En partant
d'un point de référence sur cet abaque (débit et perte de charge) il est
possible d'obtenir les pertes de charge pour des débit différents et de là,
en extraire le coefficient Cs. Cet abaque indique les pertes de charge pour
les radiateurs raccordés en diamètres 3/8", 1/2" et 3/4" et ceci pour une
longueur de référence, supérieure à 1 mètre et inférieure ou égale à 1
mètre. Pour L < 1 m et le raccordement en diamètre 1/2", Z est égal à :
Z = 35 x (D / 100)2, en Pa
Et pour L >= 1 m, Z est égal à :
Z = 45 x (D / 100)2, en Pa
Où :
100 est le débit de référence, en litres/h
D le débit réel, en litres/h
35 et 45 sont les pertes de charge en Pa pour un débit de 100 litres/h
Exemple de calcul du Cs pour :
- Radiateur :
Le radiateur mesure 1,4 m et sont débit nécessaire est de 165
litres/h, la perte de charge singulière sera de :
Z = 45 x (165 / 100)2 = 122,51 Pa
En partant de la vitesse du fluide à l'entrée du radiateur (diamètre du
raccord robinet), on peut estimer son coefficient de singularité :
Section pour le raccord du robinet en diamètre 1/2" vissé dans le radiateur
:
S = (0,015 / 2)2 x 3,1416 = 0,000177 m2
Vitesse du fluide :
v = 0,165 / 3600 / 0,000177 = 0,259 m/s
Température moyenne du fluide 60 °C, masse volumique moyenne 983 kg/m3
Cs = 122,51 x 2 / (983 x 0,2592) = 3,71
Pour un radiateur ayant une longueur de 0,8 m et un débit de 90 litres/h :
Z = 35 x (90 / 100)2 = 28,35 Pa
Cs = 28,35 x 2 / ( 983 x 0,14152) = 2,88
- Organe d'équilibrage :
1) Prenons l'abaque de la page "Les
radiateurs", on souhaite connaître le coefficient Cs pour le coude de
réglage grand ouvert, on choisi un point de référence sur la ligne GO comme
par exemple 200 litres/h pour 110 mmCE de perte de charge, pour 500 litres/h
la perte de charge sera de :
Z = 110 x (500 / 200)2 = 687,5 mmCE (6629,72 Pa)
Le coefficient Cs pour la position ouverture totale est donc de :
Section du raccord diamètre 1/2" 0,000177 m2
En mCE :
Vitesse pour 200 litres/h, v = 0,3138 m/s
Cs = 110 / 1000 x 2 x 9,81 / 0,31382 = 21,91
Vitesse pour 500 litres/h, v = 0,7846 m/s
Cs = 687,5 /1000 x 2 x 9,81 / 0,78462 = 21,91
En Pa :
Cs = 1060,75 x 2 / (983 x 0,31382) = 21,91
Cs = 6629,72 x 2 / (983 x 0,78462) = 21,91
Le coefficient de singularité pour la position grand ouvert est donc de
21,91, pour calculer la perte de charge il suffit de l'intégrer dans la
formule générale :
Z = Cs x p x v2 / 2, en Pa
Par exemple, pour 350 litres/h, v = 0,5493 m/s, la perte de charge
singulière sera de :
Z = 21,91 x 983 x 0,54932 / 2 = 3249,26 Pa (336,95 mmCE)
2)
Pour les organes de réglage comme par exemple les vannes d'équilibrage ou
encore les vannes 2, 3 ou 4 voies il est possible d'obtenir le coefficient
Cs à partir du coefficient Kv ou kvs (pour plus de précisions, voir la page
"Accessoires" paragraphe "La
vanne 2, 3 ou 4 voies"). Dans le calcul des pertes de charge de
base (pertes de charge du circuit le plus défavorisé) c'est la
position grand ouvert de l'organe qui est prise en compte donc le Kvs.
La relation entre Cs et Kv est issue de la relation de ces deux formules :
DeltaP = (D / Kv)2 x p x 100, en Pa
DeltaP = Cs x v2 / 2 x p, en Pa
Où :
D est le débit en m3/h
Kv est le coefficient de la vanne en m3/h
p est la masse volumique en kg/m3
100 pour la perte de charge en Pa (100 Pa = 1 mbar)
v est la vitesse en m/s
Donc, de la relation de ces deux formules, le coefficient de singularité Cs
est égal à :
Cs =(2 x 100) / Kv2 x (D / v)2
Cs = 200 / Kv2 x (D / v)2
Simplifions par le débit :
Avec
Di en m
La section est égale à r2 x Pi ou (Di2 x Pi) / 4 et aussi à Pi / 4 x Di2
Cs = 200 / Kv2 x (D / (D / 3600 / (Pi / 4 x Di2)))2
Cs = 200 / Kv2 x (D / D x 3600 x (Pi / 4 x Di2))2
Cs = 200 / Kv2 x (3600 x Pi / 4 x Di2)2
Cs = 200 / Kv2 x (2827,44 x Di2)2
Cs = 200 x 2827,442 x (Di2/ Kv)2
Cs = 1,5989 x109 x (Di2/ Kv)2
Avec Di en mm
Cs = 1,5989 x10-3 x (Di2/ Kv)2
Soit en arrondissant :
Cs = 0,0016 x (Di2/ Kv)2
Exemple :
Admettons une vanne 3 voies diamètre 1 1/4" (Di = 35,9 mm) avec un Kvs de 19,45 m3/h,
le coefficient Cs est égal à :
Cs = 0,0016 x (35,92/ 19,45)2 = 7,02
Attention, à chaque coefficient Kv correspond un coefficient Cs (Cs n'est
pas commun à toute la plage de réglage)
Diamètre des tubes en acier noir courants :
|
DN |
Pouce |
De (en mm) |
Di (en mm) |
| 10 |
3/8" |
17,2 |
12,5 |
| 15 |
1/2" |
21,3 |
16 |
| 20 |
3/4" |
26,9 |
21,6 |
| 25 |
1" |
33,7 |
27,2 |
| 32 |
1 1/4" |
42,4 |
35,9 |
| 40 |
1 1/2" |
48,3 |
41,8 |
| 50 |
2" |
60,3 |
53 |
| |
Diamètre intérieur en mm |
|
Cuivre |
10 |
12 |
14 |
16 |
20 |
26 |
30 |
|
38 |
|
|
Acier
|
|
12 (3/8") |
|
15 (1/2") |
20 (3/4") |
26 (1") |
|
33 (1 1/4") |
|
40 (1 1/2") |
Coude 90°
R < 1,5 D |
1,8 |
1,5 |
1,5 |
1,5 |
1 |
1 |
1 |
0,8 |
0,8 |
0,8 |
Coude 90°
R > 1,5 < 3 D |
1,8 |
1,5 |
1 |
1 |
1 |
1 |
0,7 |
0,5 |
0,5 |
0,5 |
Coude 90°
R > 3 D |
0,8 |
0,7 |
0,7 |
0,5 |
0,42 |
0,42 |
0,42 |
0,42 |
0,42 |
0,42 |
Coude 45°
R < 1,5 D |
1,2 |
1 |
1 |
0,7 |
0,7 |
0,7 |
0,7 |
0,5 |
0,5 |
0,5 |
Coude 45°
R > 1,5 < 3
D |
1,2 |
1 |
0,7 |
0,7 |
0,7 |
0,7 |
0,7 |
0,3 |
0,3 |
0,3 |
Coude 45°
R > 3 D |
0,8 |
0,6 |
0,3 |
0,3 |
0,3 |
0,3 |
0,3 |
0,2 |
0,2 |
0,2 |
|
Clapet anti-retour à ressort |
- |
- |
- |
6,7 |
7,4 |
6,2 |
- |
6,2 |
- |
6,7 |
|
Clapet anti-retour à battant |
- |
- |
- |
3,5 |
3,4 |
2,2 |
- |
2,2 |
- |
2,4 |
|
Clapet anti-thermosiphon à
ressort sur pompe |
- |
- |
- |
- |
- |
8,6 |
- |
12,6 |
- |
- |
|
Vanne à boule
|
- |
- |
- |
2,6 |
3,8 |
1,2 |
- |
1,7 |
- |
1 |
|
Vanne papillon |
- |
- |
- |
6,4 |
6,2 |
1,1 |
- |
2,3 |
- |
3,3 |
|
Vanne à opercule |
- |
0,4 |
- |
0,9 |
0,3 |
0,4 |
- |
0,7 |
- |
0,4 |
|
Vanne à clapet |
- |
3 |
- |
5 |
5 |
4 |
- |
5 |
- |
3 |
|
Vanne de réglage |
- |
- |
- |
19,6 |
12,2 |
12,8 |
- |
14,2 |
- |
14,2 |
|
 |
Méthode par estimation du
rapport J/Z.
Cette méthode n'est et de loin, pas la plus précise mais elle a l'avantage
d'être rapide. Dans un premier temps, effectuer le calcul des pertes de
charge linéiques comme indiqué plus haut, ensuite et c'est là la partie la
plus difficile, estimer le pourcentage de
pertes de charge singulières par rapport aux pertes de charge linéiques. Ceci
est à faire de façon tout à fait arbitraire donc, attention de ne pas
sous-estimer les pertes de charge singulières par rapport aux pertes de
charge linéiques.
Par exemple, dans un tronçon dérivé qui alimente un radiateur (le réseau
passe à proximité du radiateur), on peut
estimer que la perte de charge singulière totale (coude, tés, robinet,
radiateur, organe d'équilibrage) représente environ 90 à 95% des pertes de
charge totales de ce tronçon.
En partant de l'exemple, cité plus haut, admettons que ce radiateur soit piqué
sur des conduites départ/retour et que sa longueur soit de 1,1 m, la
longueur totale des conduites qui l'alimentent est de 1,2 m (coté robinet 1
m, coté coude de réglage 0,2 m) la perte de charge linéique totale est donc
de :
J = 90 x 1,2 = 108 Pa
Les conduites sur lesquelles est piqué ce radiateur ont un diamètre de 16 x
18 mm et le débit commun est de 225 litres/h :
- Perte de charge singulière du té de départ, té avec séparation des courants,
donc branche latérale :
Cs = 1 + 1 / (VLat / VCom)2
VCom = 0,225 / 3600 / (0,0082 x 3,1416) = 0,3108 m/s
VLat = 0,10202 / 3600 / (0,0062 x 3,1416) = 0,2506 m/s
Cs = 1 + 1 / (0,2506 / 0,3108)2 = 2,54
Z = 2,54 x 983,25 x 0,25062 / 2 = 78,42 Pa
- Perte de charge singulière du té de retour, té avec réunion des courants,
donc branche latérale
:
Cs = (1 - 0,66 x (0,012 / 0,016)2 + 0,26 x (0,012
/ 0,016)2)2 x (1 + 2 x (0,012 /
0,016)2 / (0,2506 / 0,3108) - 1 / (0,2506
/ 0,3108)2) = 0,5148
Z = 0,5148 x 983,25 x 0,25062 / 2 = 15,89 Pa
- Perte de charge du coude raccordé sur le robinet :
Z = 1,5 x 983,25 x 0,25062 / 2 = 46,31 Pa
- Perte de charge du robinet en diamètre 1/2" :
Z = 55 x 983,25 x 0,25062 / 2 = 1698,08 Pa
- Perte de charge du coude de réglage en diamètre 1/2" :
Z = 35 x 983,25 x 0,25062 / 2 = 1080,6 Pa
- Perte de charge du radiateur :
Z = 3,71 x 983,25 x 0,25062 / 2 = 114,54 Pa
Les pertes de charge singulières totales sont de :
Z = 78,42 + 15,89 + 46,31 + 1698,08 + 1080,6 + 114,54 = 3033,84 Pa
Et les pertes de charge totales de ce radiateur s'élèvent à :
DeltaP = 108 + 3033,84 = 3141,84 Pa
Les pourcentages de pertes de charge pour J et Z sont respectivement de :
J = 108 / 3141,84 x 100 = 3,44%
Z = 3033,84 / 3141,84 x 100 = 96,56%
Le rapport J/Z est donc de :
J/Z = 3,44 / 96,56 = 0,0356
Donc, à partir des pertes de charge linéiques et en appliquant ce rapport,
on peut estimer les pertes de charge totales :
DeltaP = 108 + 108 / 0,0356 = 3141,7 Pa
Maintenant, si ce radiateur est raccordé en hydraucâblé en PER diamètre 13 x
16 mm à partir d'un collecteur avec une longueur totale de tube de 10 m
environ (départ/retour), le rapport sera de l'ordre de 0,25 (J 20%, Z 80%)
Une idée de rapport pour certains raccordements :
Partie chaudière et accessoires, on peut estimer un pourcentage J/Z de
10/90%
Réseau de distribution principal, 70/30%
Réseau de distribution secondaire, 60/40%
Les radiateurs piqués au passage, 5/95%
Le dernier radiateur en bout de circuit, 20/80%
En raccordement hydraucâblé, 25/75%
Circuit d'alimentation avec collecteurs pour radiateurs 45/55%
Circuit d'alimentation avec collecteurs pour plancher chauffant 35/65%
|
 |
Outils.
Pour cette méthode, un classeur Excel est disponible en téléchargement à la
page "Classeur pertes de charge J-Z"
|
|
|
 LES PERTES DE CHARGE
LES PERTES DE CHARGE LES PERTES DE CHARGE
LES PERTES DE CHARGE