 |
La vanne
2, 3 ou 4 voies.
Le dimensionnement d'une vanne 2, 3 ou 4 voies n'est pas aussi simple
qu'il y paraît. Pour dimensionner une vanne, il est nécessaire de connaître
plusieurs paramètres comme le coefficient Kv de la vanne, la perte de charge
de la vanne, la courbe caractéristique de celle-ci, la perte de charge du
circuit à débit variable (la partie où il n'y a pas le circulateur pour une
vanne 3 ou 4 voies), etc. Il
n'est pratiquement pas possible de dissocier une vanne du circuit sur lequel
elle est montée car certaines de ses caractéristiques sont étroitement liées
avec celles du circuit. Deux vannes identiques montées sur deux circuits
différents ne donneront pas les mêmes résultats.
Il existe plusieurs type de vannes, vannes à caractéristiques linéaires
(débit proportionnel à la course H), vannes à caractéristiques quadratiques
(débit proportionnel au carré de la course H), vannes à caractéristiques
logarithmiques dites aussi à égal pourcentage (la Course H du clapet produit une
variation proportionnelle au débit total précédent le changement).
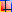 |
Le
coefficient Kv.
Le coefficient Kv caractérise la capacité d'une vanne 2, 3 ou
4 voies. Ce coefficient indique le débit en m3/h pour une perte de pression (perte de charge) de 1 bar (10,193 mCE)
et une température d'eau d'environ 4°C, la course de la vanne étant
quelconque, H = x%.
On désigne par KvS la valeur du Kv pour une course H = 100%
(vanne grande ouverte). C'est cette valeur qui est indiquée sur les
catalogues des fabricants.
Le fabricant le détermine de
façon expérimentale. La vanne est montée sur un banc d'essai où une
pompe met de l'eau en circulation, le débit est ensuite adapté de façon
à obtenir une chute de pression de 1 bar entre l'amont et l'aval de la
vanne (des prises de pressions sont montées de part et d'autre de
celle-ci), une fois cette chute obtenue, il ne suffit plus qu'à lire le
débit en m3/h sur le débitmètre.
On désigne par Kv0 la valeur du Kv pour une course H = 0
(vanne fermée) avec
la même perte de pression (1 bar). Cette valeur est donné par le
fabricant et représente généralement le débit de fuite, souvent donnée
en % de KvS.
Pour obtenir le Kv (ou KvS), on utilise la formule suivante :
Kv (ou KvS) = D x RACINE(p / (DeltaPV x 1000))
ou :
Kv (ou KvS) = D x (p / (DeltaPV x 1000))0,5
D est le débit en m3/h
p est la masse volumique du fluide en kg/m3 fonction de la
température (voir page "Formule
et Tableaux")
DeltaPV est la perte de charge de la vanne en bar
Partant de cette formule, il est possible de connaître le débit :
D = Kv x RACINE((DeltaPV x 1000) / p)
et de là, la perte de charge de la vanne :
DeltaPV = p x (D / Kv)2 / 1000
Exemple, admettons une vanne ayant un coefficient Kv de 3,5 m3/h,
quel sera son débit pour une masse volumique de l'eau de 983,13 kg/m3
(60°C) et une perte de charge 0,01 bar (0,10193 mCE) ?
D = 3,5 x RACINE((0,01 x 1000) / 983,13) = 0,352 m3/h
(352 litres/h)
|
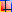 |
L'autorité
de la vanne aV.
La fonction première d'une vanne est d'assurer la progressivité du
débit et plus important encore, dans le cas qui nous intéresse, la
progressivité de la puissance thermique. Par progressivité, on entend augmentation ou diminution régulière du débit ou de la
puissance thermique. Cette progressivité sera fonction de l'autorité (ou efficacité) de la vanne, notée aV
(ou seulement a ou encore PV), représentant
le rapport de la perte de charge de la vanne grande ouverte, H = 100%, à
la perte de charge du circuit à débit variable. Ce rapport est obtenu de
la manière suivante :
aV = DeltaPV / (DeltaPV + DeltaPCircuit)
DeltaPV est la perte de charge de la vanne sur le circuit où
elle se trouve et grande ouverte, H = 100%
DeltaPCircuit est la perte de charge du circuit à débit
variable
Partant de cette formule, il est possible de connaître la perte de
charge du circuit à débit variable :
DeltaPCircuit =
DeltaPV /
aV - DeltaPV
ainsi que la perte de charge de la vanne :
DeltaPV =
aV / (1 -
aV) x DeltaPCircuit
L'autorité
aV varie entre 0 et 1 sans jamais atteindre ces
extrémités car pour cela, la vanne devrait avoir, soit une perte de
charge égale à 0, soit une perte de charge infinie.
La vanne mélangeuse ne peut disposer que d'une partie de la perte de
charge totale et c'est son autorité qui détermine la forme des courbes
caractéristiques. Pour pouvoir réguler facilement le débit, l'autorité
de la vanne doit être comprise entre 0,25 et 0,7, 0,5 étant la valeur
moyenne correspondant à une perte de charge pour la vanne égale à celle
du circuit à débit variable.
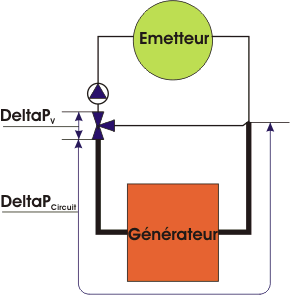
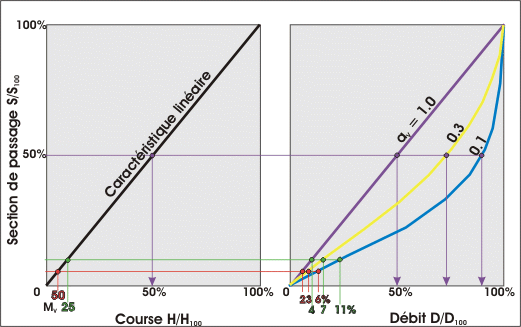
Les graphiques ci-dessous représentent les courbes caractéristiques en
fonction de l'autorité
aV, d'une vanne à caractéristique linéaire et
d'une vanne à caractéristique logarithmique. Pour ces graphiques, Kv0
est égal à 2% du KvS.
- Pour une vanne à caractéristique linéaire, la formule suivante permet de calculer les courbes caractéristiques à
perte de charge constante en fonction de l'autorité
aV :
D/D100 = 1 / RACINE(1 +
aV x ((KvS / Kv)2
- 1))
La courbe caractéristique d'une vanne est la relation qui lie le
coefficient Kv à la course. Dans le cas d'une caractéristique linéaire,
les variations de la course restent proportionnelles à celles du
coefficient Kv. Dans ce cas, la formule ci-dessus peut s'écrire :
D/D100 = 1 / RACINE(1 +
aV x (1 / h2 - 1))
h étant le pourcentage de la course (de 0 à 1), h = H / H100
Exemple avec une autorité
aV de 0,50, un KvS de 12, un Kv0
de 0,24 et une course de 50% :
h = 0,5
D/D100 = 1 / RACINE(1 + 0,50 x (1 / 0,52 - 1)) =
0,632 (63,2%)
Avec une autorité de 0,1 et toujours avec une course de 50% :
D/D100 = 1 / RACINE(1 + 0,10 x (1 / 0,52 - 1)) =
0,877 (87,7%)
-
Pour une vanne à caractéristique logarithmique, la formule est un peu
plus complexe :
D/D100 = 1 / RACINE(1 +
aV x (((KvS / Kv0)
/ EXP(Ln(KvS / Kv0) x h))2 - 1))
EXP, fonction inverse de Ln (ex ou e^ sur les calculatrices)
Ln, logarithme népérien
Exemple avec une autorité
aV de 0,50, un KvS de 12, un Kv0
de 0,24 et une course de 50% :
D/D100 = 1 / RACINE(1 + 0,5 x (((12 / 0,24) / EXP(Ln(12 /
0,24) x 0,5))2 - 1)) =
0,198 (19,8%)
Avec une autorité
aV de 0,1 et toujours avec une course de 50% :
D/D100 = 1 / RACINE(1 + 0,1 x (((12 / 0,24) / EXP(Ln(12 /
0,24) x 0,5))2 - 1)) =
0,411 (41,1%)
A partir des formules précédentes, connaissant le pourcentage de débit,
il est possible de déterminer la course correspondante (formules
inverses) :
- pour une vanne à caractéristique linéaire :
H/H100 = 1 / ((((1 /
D/D100)2 - 1) / aV + 1)0,5)
- pour une vanne à caractéristique logarithmique :
H/H100 = ln((KvS / Kv0)
/ ((((1 /
D/D100)2 - 1) / aV + 1)0,5))
/ ln(KvS / Kv0)
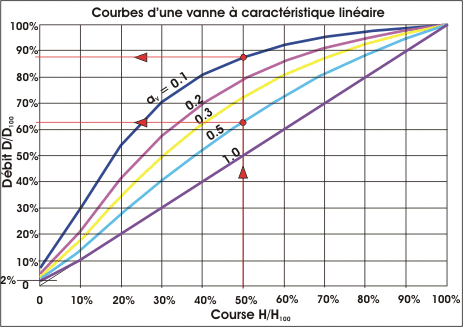
Il est déconseiller d'utiliser une autorité
aV supérieure à 0,7 car la perte de charge engendrée sera
trop importante et ceci obligera le choix d'un circulateur plus puissant
que nécessaire d'où une augmentation inutile du coût d'exploitation. Le
second inconvénient sera les risques de bruits causés par l'augmentation
importante de la vitesse du fluide dans le corps de vanne, vitesse qui
pourra causée une érosion prématurée du corps de vanne. Il est de même
déconseillé d'utiliser une autorité aV inférieure à 0,25 car dans la zone de fermeture de la
vanne la régulation devient instable (pour des raisons constructives),
généralement en dessous de Kv0 et donc, ce comportement est
amplifié par le surdimensionnement de la vanne (débit de fuite plus
important). Ceci induit aussi un débit plus important à chaque impulsion
envoyée par la régulation, débit qui risque d'être trop important selon
la durée de l'impulsion, ce qui risque d'entraîner un pompage (ordres et
contre-ordres successifs). On peut constater ceci sur les deux graphiques ci-dessous
concernant les vannes à caractéristique linéaire et
les vannes à caractéristique logarithmique pour les
courbes de puissance thermique correspondant à une autorité de 0,1. On
peut voir que la puissance thermique est déjà trop importante dans la
zone de fermeture et ceci va entraîner un déséquilibre thermique du
logement et donc une instabilité de la régulation du système.
|
 |
Le
rapport de réglage ou marge de réglage MV.
C'est le rapport du débit maximal (KvS) pour une course H
= 100% au débit minimal (Kv0) pour une course H = 0 (qui
dépend des tolérances de fabrication) MV = KvS / Kv0.
Les valeurs habituelles se situent entre 20 et 100 avec une moyenne
générale plutôt près de 50. Pour l'exemple d'où sont issus les graphiques ci-dessus,
le rapport de réglage est égal à :
MV = 12 / 0,24 = 50
Plus le rapport de réglage est faible, plus la régulation sera instable
dans la zone de fermeture, ce qui entraînera un déséquilibre thermique, phénomène qui sera amplifié par le choix
d'une trop faible autorité aV (vanne surdimensionnée).
Le croquis ci-dessous n'est pas à l'échelle mais il illustre bien le
sujet, si le rapport de réglage diminue (vanne de moins bonne qualité),
la valeur de Kv0 augmente et plus l'autorité est faible, plus
le débit dans la zone de fermeture augmente rendant la régulation de
plus en plus instable.
|
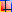 |
Rapport
entre course de la vanne et puissance thermique.
Dans l'utilisation que l'on fait en chauffage d'une vanne mélangeuse et tout particulièrement en chauffage pour logement
individuel, c'est en général la
proportionnalité puissance thermique / course qui est recherchée plutôt
que la proportionnalité débit / course car la puissance thermique n'est
pas proportionnelle au débit. Le graphique ci-dessous le montre bien
(voir "vanne à caractéristique logarithmique"), avec
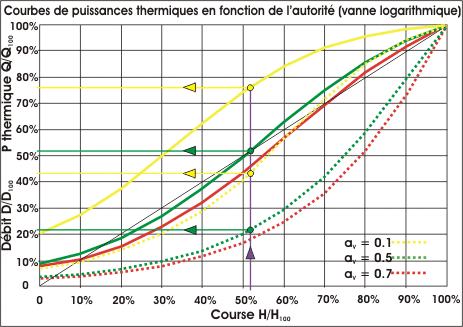
une autorité
aV de 0,1 (trait en pointillé jaune) le débit est
relativement proportionnel à la course mais on voit bien que la courbe
de puissance thermique correspondante (trait plein en jaune) ne l'est pas
du tout puisque pour une course de 50% la puissance thermique est déjà
de 75% alors que pour une autorité de 0,5 le débit n'est pas
proportionnel mais la puissance thermique l'est, 50% de course donne 50% de
puissance thermique pour 20% de débit.
C'est bien à cause de cette non proportionnalité entre débit et
puissance thermique qu'il est nécessaire d'adopter une autorité de vanne
suffisante pour réguler au mieux le débit dans la zone de fermeture. Il
en va de même pour la qualité d'usinage de la vanne, le rapport de
réglage doit être aussi élevé que possible, au minimum 50 voir même 100, afin d'avoir
le moins de débit parasite (fuite) pour une course H = 0.
Dans les deux paragraphes suivants, un exemple est utilisé afin de mieux
illustrer ce qui vient d'être dit.
 |
Vanne à caractéristique linéaire.
Admettons un logement chauffé par radiateurs avec un coefficient H de 250 W/K (voir la partie concernant les calculs des
déperditions thermiques), la
température moyenne du logement est de 20°C et la température extérieure
de base de -9°C. Les déperditions thermiques dans les conditions
extérieures de base sont de :
Dep = 250 x (20 - -9) = 7250 W (7,25 kW)
Le débit nécessaire avec une chute (DeltaT) de température dans les
radiateurs de 10°C est de :
D = 7250 / (1,1628 x 10) = 623,4 l/h
La vanne a un KvS de 12 m3/h et un Kv0
de 0,24 m3/h soit un rapport de réglage MV =
50.
Les émetteurs sont normalisés (température de départ (Td) = 75°C,
température de retour (Tr) = 65°C et température ambiante du logement (Ti)
= 20°C).
Note : Il faut savoir que la chute (DeltaT) dans les radiateurs n'est
pas constante, si on réduit la température de départ ou que l'on
diminue sensiblement le débit, la pièce étant toujours à la même
température, la température de retour peut avoir des valeurs
différentes. Si on maintient la chute constante dans les calculs, à un
moment donné la température de retour sera inférieure à la température
ambiante de la pièce, exemple : Td = 28°C, Ti = 20°C Tr = 28 - 10 =
18°C. Comme il s'agit d'une impossibilité physique, la température de
retour sera forcément supérieure ou égale à celle de la pièce. Avec une
chute définie à 10°C pour une température de départ de 75°C, la formule
empirique suivante donne la température de retour approximative en
fonction de la température de départ radiateurs, du débit et la température
ambiante de la pièce :
Tr = Td x EXP(-H / (D x 2)) + Ti x (1 - EXP(-H / (D x 2)))
Ceci dit, admettons maintenant que la température extérieure (Te) soit
de 5°C, les déperditions thermiques dans ces conditions sont alors de :
Dep = 250 x (20 - 5) = 3750 W (3,75 kW)
La température de départ nécessaire n'étant plus de 75°C et comme la
température de retour est fonction de celle de départ, des itérations
successives entre la formule précédente et la suivante sont nécessaires
:
Td = (Dep / DepBase)(1/1,287) x 50 + Ti + (Td -
Tr) / 2
On trouve alors :
Td = (3750 / 7250)(1/1,287) x 50 + 20 + (52,95 - 46,96) / 2 = 52,95°C
Tr = 52,95 x EXP(-250 / (623,4 x 2)) + 20 x (1 - EXP(-250 / (623,4 x 2))) =
46,96°C
En
admettant une température constante de 75°C coté chaudière, ce qui n'est
plus le cas avec les nouvelles régulations car elles adaptent la
température d'eau de chaudière en fonction des besoins de chaleur, le débit d'eau
à 75°C en provenance de la chaudière est obtenu avec la formule suivante
:
DCh = D x ((Td - Tr) / (TdCh -
Tr))
TdCh = température du fluide en provenance de la
chaudière
DCh = 623,4 x ((52,95 - 46,96) / (75 - 46,96)) =
133,173 l/h
Vérification :
Td =
(75 x 133,173 + 46,96 x 490,227) / 623,4 = 52,95°C
Le débit d'eau en provenance de la chaudière est donc de 133,173 l/h et le
débit recyclé de 490,227 l/h.
Avec une vanne à caractéristique linéaire, si le débit
était proportionnel à la course, celle-ci devrait être de :
H/H100 = 133,173 / 623,4 x 100 = 21,36%
Pour avoir cette proportionnalité, l'autorité de la vanne devrait être
égale à 1 mais
ceci est impossible car la perte de charge serait alors infinie, donc, en
prenant une autorité de 0,7 (qui est une valeur élevée, que l'on
considère même comme valeur limite) et afin d'avoir 21,36% de débit en
provenance de la chaudière, la course devra être seulement de :
H/H100 = 1 / ((((1 / 0,2136)2 - 1) / 0,7 + 1)0,5)
= 0,1799 soit 18% de course.
Maintenant, admettons malgré tout que la vanne s'ouvre de 21,36% le
pourcentage de débit est alors
de :
D/D100 = 1 / RACINE(1 + 0,7 x (1 / 0,21362 - 1)) = 0,2528
soit 25,28%
Soit un débit de :
D = 623,4 x 0,2528 = 157,6 l/h
La température de départ change et passe à :
Ceci demande la résolution d'une équation.
Equation :
623,4y - 465,8z = 75 x 157,6
Constantes (pour cet exemple) pour le calcul de la température de
retour :
EXP(-250 / (623,4 x 2)) = 0,8183
20 x (1 - EXP(-250 / (623,4 x 2))) = 3,634
z = y x 0,8183 + 3,634
L'équation devient :
623,4y - 465,8 x (y x 0,8183 + 3,634) = 11820
623,4y - 465,8y x 0,8183 - 465,8 x 3,634 = 11820
242,24y - 1692,72 = 11820
242,24y = 13512,72
y = 13512,72 / 242,24 = 55,78°C
Donc :
z = 55,78 x 0,8183 + 3,634 = 49,28°C
Vérification :
Td = (75 x 157,6 + 49,28 x 465,8) / 623,4 = 55,78°C
Avec une température de départ de 55,78°C et des déperditions thermiques
de 3750 W le logement sera en déséquilibre thermique (trop d'émissions
par rapport aux déperditions). La température ambiante pour atteindre
l'équilibre thermique sera de :
Q = 7250 x ((((55,78 + 49,28) / 2) - 20) / 50)1,287 = 4169,4
W
Ti = 4169,4 / 250 + 5 = 21,68°C
La température réelle sera en fait de 21,04 °C. Des itérations
successives sont à faire entre les 3 formules où la température de la
pièce intervient afin d'obtenir la
température d'ambiance.
Pour conserver l'équilibre thermique dans le logement, la course de la
vanne devra donc bien être égale à 18%. La puissance thermique n'étant pas
proportionnelle au débit, elle sera alors de :
Q/Q100 = 3750 / 7250 x 100 =
51,72% pour un débit de 21,36% et une course de 18%. On peut constater que
la moitié de la puissance thermique est déjà disponible pour un
cinquième de la course de la vanne. Ceci réduit de façon significative la plage de réglage de la vanne. Avec une autorité
de 0,1 (voir graphique ci-dessous), les 18% de course donne 50% de débit
et déjà 80% de la puissance thermique. On peut voir aussi que les 51,72% de puissance thermique
sont déjà atteints avec une course de seulement 8%.
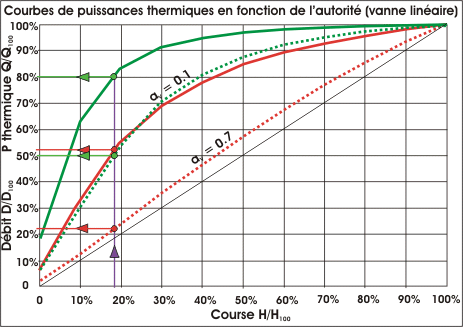
Sachant qu'il est conseillé de ne pas dépasser une autorité de 0,7, ceci démontre que pour avoir une
régulation progressive de la puissance thermique, la vanne à
caractéristique linéaire n'est pas la mieux adaptée si la température de
chaudière est maintenue supérieure à 70°C.
Comme il est dit plus haut, les régulations actuelles peuvent aussi
gérer la température de chaudière et l'adapter aux besoins de chaleur en
fonction de la température extérieure (ce qui a déjà l'avantage de
limiter les pertes thermiques de la chaudière et des conduites la
raccordant). La température de chaudière est maintenue à environ 8°C en
moyenne au dessus de la température de départ émetteurs nécessaire,
différentiel qu'il est possible de régler selon le régulateur
utilisé.
Reprenons l'exemple ci-dessus, la température de départ nécessaire étant
de 52,95°C, la régulation va maintenir la température moyenne de la
chaudière à environ 61°C. Le débit en provenance de la chaudière n'est
alors plus de 133,173 l/h à 75°C mais de 265,97 l/h à 61°C ce qui fait
passer le pourcentage de débit de 21,36% à 42,66% et dans ce cas, la
course, avec une autorité de 0,7, est de :
H/H100 = 1 / ((((1 / 0,4266)2 - 1) / 0,7 + 1)0,5)
= 0,367 soit 36,7%
De ce fait, la plage de réglage de la vanne s'élargie et par là, la
progressivité du débit et de la puissance thermique.
|
 |
Vanne à caractéristique logarithmique.
En partant de l'exemple précédent (pour pouvoir comparer plus
facilement) avec température de chaudière
constante à 75°C. La température de départ radiateurs pour une
puissance thermique de 3750 W étant de 52,95°C, le débit nécessaire
venant de la chaudière à 75°C est de 133,173 l/h, ce qui donne
21,36% de débit. Avec une vanne à caractéristique logarithmique,
prenons comme valeur pour l'autorité aV, la même que précédemment,
soit aV = 0,7. La course est alors de :
H/H100 = ln((12 / 0,24) / ((((1 / 0,2136)2 - 1) /
0,7 + 1)0,5)) / ln(12 / 0,24) = 0,5616 soit 56,16%
Toujours pour un pourcentage de puissance thermique de :
3750 / 7250 x 100 = 51,72%.
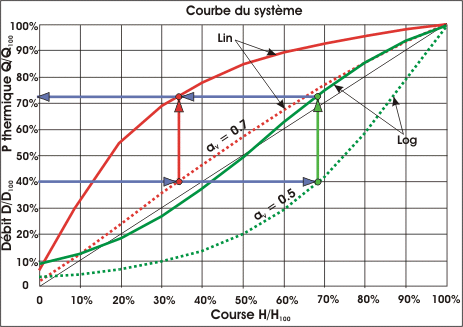
Sur le graphique ci-dessous on peut voir que la progressivité de la puissance thermique,
pour les autorités de 0,7 et 0,5 (traits continus rouge et vert), est sensiblement la même, on
préfère donc une autorité de 0,5, ce qui permet de limiter la HM du
circulateur et les éventuels bruits. La course est alors de :
H/H100 = ln((12 / 0,24) / ((((1 / 0,2136)2 - 1) /
0,5 + 1)0,5)) / ln(12 / 0,24) = 0,5197 soit 51,97%
Maintenant, en admettant, comme pour la vanne à caractéristique
linéaire, que la régulation module la température de chaudière, le
pourcentage de débit est alors de 42,66% et dans ce cas, la course,
avec une autorité de 0,5, est de :
H/H100 = ln((12 / 0,24) / ((((1 / 0,4266)2 - 1) /
0,5 + 1)0,5)) / ln(12 / 0,24) = 0,7058 soit 70,58%
Pour rendre plus proportionnelle la puissance thermique, on peut
adopter une autorité plus faible, avec une autorité de 0,3 la course
est alors de :
H/H100 = ln((12 / 0,24) / ((((1 / 0,4266)2 - 1) /
0,3 + 1)0,5)) / ln(12 / 0,24) = 0,6457 soit 64,57%
Si on décide d'adopter une autorité plus faible, en contre partie,
le rapport de réglage devra être plus élevé afin de ne pas rendre la
régulation instable dans la zone de fermeture.
Note : les courbes de puissance thermique sont tracées avec une
température de chaudière constante de 75°C.
Les deux graphiques ci-dessus représentent les courbes caractéristiques de la
vanne en fonction de l'autorité (traits en pointillés) ainsi que les
courbes caractéristiques du système correspondantes (traits pleins).
La formule suivante nous permet de cerner approximativement
l'évolution de la courbe caractéristique du système :
Q/Q100 = 1 / (1 + a x ((1 - D/D100) / D/D100))
a étant le coefficient du système qu'il est possible d'obtenir à
partir d'un premier résultat avec la formule inverse :
a = (1 / Q/Q100 - 1) / ((1 - D/D100) / D/D100)
En partant de l'exemple précédant, le coefficient a est de :
a = (1 / 0,5172 - 1) / ((1 - 0,2136) / 0,2136) = 0,2535
A partir de là, il est possible de connaître le pourcentage de
puissance en fonction du pourcentage de débit. Donc par exemple,
pour 40% de débit,
la puissance délivrée est de :
Q/Q100 = 1 / (1 + 0,2535 x ((1 - 0,4) / 0,4)) = 0,7245
soit :
7250 x 0,7245 = 5252,63 W pour 623,4 x 0,4 = 249,36 l/h à 75°C en
provenance de la chaudière.
Résultat qui est représenté graphiquement ci-dessous pour vanne à
caractéristique linéaire et logarithmique.
 |
Une vanne à caractéristique linéaire peut être utilisée en
régulation de chauffage mais avec une forte autorité et une régulation
de la température de chaudière. Dans le cas contraire, la plage de
réglage sera trop réduite et la régulation du
logement sera instable, la température ambiante oscillant de
manière significative autour de la valeur de consigne.
Pour compenser ce phénomène de non linéarité de la puissance
thermique il faut utiliser une vanne ayant un comportement non linéaire
inversé du pourcentage du débit et dans ce cas, les vannes à caractéristique
logarithmique sont les plus intéressantes car la proportionnalité puissance thermique / course est la
meilleure. Si la régulation module la température de chaudière,
l'autorité de la vanne peut être inférieure à 0,5, mais de toute
façon, on aura soins de choisir une vanne de qualité ayant un
rapport de réglage assez élevé, au minimum 50 voir même 100, afin de limiter
l'instabilité de la régulation dans la zone de fermeture.
|
 |
Exemple
de dimensionnement.
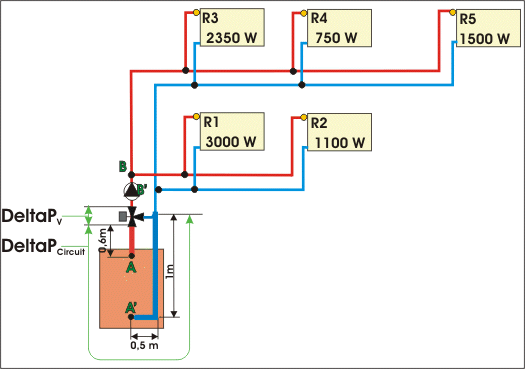
Admettons qu'une vanne 3 voies doit être
installée sur l'installation prise en exemple à la page "Les
radiateurs". La partie du circuit à débit variable est matérialisée en gras
sur le croquis ci-dessous (partie chaudière, donc sans circulateur). La
perte de charge de cette partie du circuit est de :
J = 6 mmCE/m, Z = 4,91
mmCE/m donc, DeltaPCircuit = (6 + 4,91) x (0,6 + 1 + 0,5) = 22,91
mmCE soit 22,91 / 10193 = 0,00224 bar.
- Avec une vanne à caractéristique linéaire.
En appliquant, comme donnée d'entrée, une autorité aV de 0,7, la perte de
charge de la vanne est de :
DeltaPV = 0,7 / (1 - 0,7) x 0,00224 = 0,00523 bar.
Le débit total de l'installation passant par la vanne grande ouverte (H =
100%) est de 0,614 m3/h,
en admettant une température moyenne de l'eau (sur la saison de chauffe) de 50°C, la masse volumique de
l'eau est de 988,04 kg/m3, le KvS de la vanne pour déterminer le
choix dans le catalogue du fabricant est de :
KvS = 0,614 x RACINE(988,04 / (0,00523 x 1000)) = 8,43 m3/h.
Dans le catalogue d'un fabricant (ici Danfoss), le choix, en première
approche, se porte sur une vanne ayant un KvS immédiatement
supérieur à 8,43 m3/h. On trouve la vanne de type HRE3 DN25 (1") avec un KvS
de 12 m3/h. Avec un KvS de 12 m3/h, la
perte de charge ne sera pas de 0,00523 bar mais de :
DeltaPV = 988,04 x (0,614 / 12)2 / 1000 = 0,00259 bar
d'où une autorité de :
aV = 0,00259 / (0,00224 + 0,00259) = 0,54
La valeur de l'autorité est correcte mais la progressivité du débit et
donc de la puissance thermique ne sera pas optimale pour ce type de
vanne, alors voyons avec le modèle inférieur. Le modèle en dessous, HRE3 DN20 (3/4"), a un KvS de 8 m3/h. Ceci nous donne
comme perte de charge pour le vanne de :
DeltaPV = 988,04 x (0,614 / 8)2 / 1000 = 0,0058 bar
l'autorité est de :
aV = 0,0058 / (0,00224 + 0,0058) = 0,72
Comme le rapport de réglage MV est un facteur de choix, il
est nécessaire d'en connaître la valeur.
Pour une course H = 0, le Kv0 est égal à 1% de
KvS, soit, pour tous les modèles dans ce type de vanne mais
avec les valeurs du modèle HRE3 DN20 (3/4") :
Kv0 = 8 x 0,01 = 0,08
MV = 8 / 0,08 = 100
La vanne étant de bonne voir de très bonne qualité de fabrication, il
est possible d'utiliser les 2 modèles mais comme la vanne est à
caractéristique linéaire, il est préférable d'adopter le modèle HRE3
DN20 (3/4"). La valeur de son autorité étant supérieure à la valeur limite (0,7) mais malgré tout
très proche, elle offre une meilleure progressivité du débit et par là,
de la puissance thermique.
- Avec une vanne à caractéristique logarithmique.
Autorité choisie comme donnée d'entrée, aV = 0,5, la perte de charge
pour une cette autorité est de :
DeltaPV = 0,5 / (1 - 0,5) x 0,00224 = 0,00224 bar soit égale à
celle du circuit à débit variable.
le KvS de la vanne pour déterminer le
choix est de :
KvS = 0,614 x RACINE(988,04 / (0,00224 x 1000)) = 12,89 m3/h.
Toujours dans le même catalogue, le choix se porte sur le type de vanne VR3 DN32
(11/4") avec un KvS
de 16 m3/h.
La perte de charge ne sera pas de 0,00224 bar mais de :
DeltaPV = 988,04 x (0,614 / 16)2 / 1000 = 0,00146 bar
d'où une autorité de :
aV = 0,00146 / (0,00224 + 0,00146) = 0,39
L'autorité est correcte mais voyons la valeur avec le modèle inférieur. Ce
modèle est le type VR3 DN25 (1") avec un KvS de 10 m3/h.
La perte de charge est de :
DeltaPV = 988,04 x (0,614 / 10)2 / 1000 = 0,00372 bar
d'où une autorité de :
aV = 0,00372 / (0,00224 + 0,00372) = 0,62
Comme nous l'avons vu sur le graphique plus haut (en partie seulement et
pour
aV = 0,5 et 0,7), la courbe du système
est relativement proportionnelle à la course. Pour cette
proportionnalité, la plage d'autorité
va de 0,3 à 0,7, dans ce cas, les deux modèles de vanne conviennent pour
l'installation. Ici c'est le rapport de réglage qui va aider à faire le
choix. Si le rapport de réglage est plutôt faible (MV < 50) on choisira
la vanne ayant l'autorité la plus élevée de façon à ne pas amplifier
l'instabilité dans la zone de fermeture, si par contre le rapport de
réglage est assez élevé (MV >= 50), on préfèrera la vanne
ayant l'autorité la plus faible afin de limiter l'augmentation de la
perte de charge de base servant au dimensionnement du circulateur sans
pour autant amplifier l'instabilité de la régulation dans la zone de
fermeture.
Pour une course H = 0 et pour ce type de vanne, le Kv0 est
égal à 0,1% de
KvS, soit, avec les valeurs du modèle VR3 DN32 (11/4")
:
Kv0 = 16 x 0,001 = 0,016 m3/h
Ceci nous donne un rapport de réglage de :
MV = 16 / 0,016 = 1000
Avec un type de vanne d'une telle qualité, le choix se porte sans
hésitation sur le modèle ayant l'autorité la plus faible, donc le modèle
VR3 DN32 (11/4").
Comme une vanne 3 voies a été rajoutée au circuit, la perte de charge de base
va augmenter, elle passe de 1000 mmCE si la perte de charge artificielle n'a
pas été rajoutée pour compenser la perte de charge résultante (100,49
mmCE) sinon, de 899,51 mmCE à :
avec la vanne à caractéristique linéaire :
0,0058 x 10193 = 59,12 mmCE
899,51 + 59,12 = 958,63 mmCE
(0,0940 bar)
avec la vanne à caractéristique logarithmique :
0,00146 x 10193 = 14,88 mmCE
899,51 + 14,88 = 914,39 mmCE
(0,0897 bar).
La perte de charge disponible en vitesse 1 pour le débit de 614 l/h
étant de 1250 mmCE et ceci en n'ayant pas créé de perte de charge
artificielle pour arrivée à 899,51 mmCE aucun
problème, sinon, une simple rectification de la valeur de cette perte de
charge artificielle sera à faire. Dans le cas contraire, un rééquilibrage serait à faire en
choisissant, dans le cadre de l'exemple, une vitesse supérieure (vitesse
2) ou alors un circulateur plus puissant si cela s'averrait nécessaire.
L'exemple montre bien l'interdépendance vanne/circuit.
Pour un dimensionnement rapide, il est possible de prendre, pour la
vanne, un diamètre au dessous du diamètre
des conduites de départ et retour chauffage (Voir la page "Les radiateurs" pour
définir les diamètres), ceci afin d'avoir un réglage plus fin. Une vanne en
1/2" sera utilisée si le départ est en 3/4" ou 20x22, une vanne en 3/4" sera
utilisée si le départ est en 1" ou 26x28 et une vanne en 1" sera utilisée si
le départ est en 11/4" ou 30x32. Cette règle empirique a donnée
satisfaction dans la pratique mais elle n'aura jamais l'efficacité d'un
dimensionnement par calcul. Pour preuve, la vanne à caractéristique
linéaire choisie dans l'exemple précédent a un DN égal aux tuyaux la
raccordant (cuivre de diamètre 20x22) et celle à caractéristique
logarithmique a un DN supérieur à ces derniers. Comme le diamètre des
tuyaux au départ de la chaudière est fonction de la façon dont on a
conduit les calculs de pertes de charge et de la manière arbitraire du
choix des diamètres tout au long du circuit le plus défavorisé
(l'exemple en est donné pour le calcul du tronçon AB B'A'), il ne faut
pas se fier aveuglément à cette règle.
|
|
 LES ACCESSOIRES
LES ACCESSOIRES LES ACCESSOIRES
LES ACCESSOIRES